Преди да се задълбочим в основната ни задача, формиране на знания и умения за решаване на различни видове задачи с подобни триъгълници, малко трябва да кажем или да припомним за еднакви триъгълници.

Определение за еднакви триъгълници:

Признаци:

I признак:

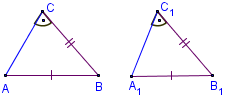
Два триъгълника са еднакви, ако две страни и ъгъл заключен между тях от един триъгълник са съответно равни на две страни и ъгъл заключен между тях от друг триъгълник.
Ако AB = A₁B₁, AC = A₁C₁BAC = B₁A₁C₁, то ΔABC ≅ΔA₁B₁C₁

II признак:

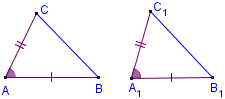
Два триъгълника са еднакви, ако страна и два ъгъла от един триъгълник са съответно равни на страна и два ъгъла от друг триъгълник.
Ако AB = A₁B₁, ∠BAC = ∠B₁A₁C₁ и ∠ABC =∠A₁B₁C₁,
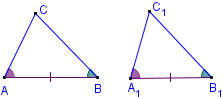
то ΔABC ≅ ΔA₁B₁C₁

III признак:

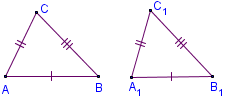
Два триъгълника са еднакви, ако три страни от един триъгълник са съответно равни на три страни от друг триъгълник.
Ако AB = A₁B₁, BC = B₁C₁ и AC = A₁C₁, то ΔABC ≅ ΔA₁B₁C₁

IV признак:

Два правоъгълни триъгълника са еднакви, ако катет и хипотенуза от един триъгълник са съответно равни на катет и хипотенуза от друг триъгълник.
Ако BC = B₁C₁ и AB = A₁B₁, и ∠ACB = ∠A₁C₁B₁ = 90°, то ΔABC ≅ ΔA₁B₁C₁