-
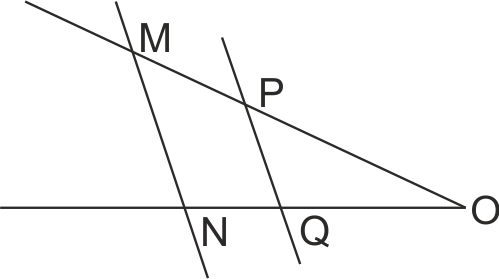
На чертежа 1 ∠NOM, MN || PQ, OM = 12, OP = 9, OQ = 4. Отсечка NQ е равна на:
3/4
4/3
4
9/12
-
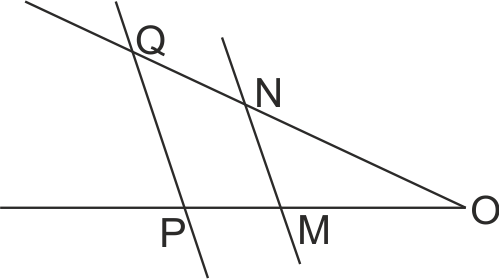
На чертежа 2 ∠POQ, MN || PQ, OM = 6, ON = 8, NQ = 6. Отсечка MP е с дължина:
2/9
9
4,5
12
-
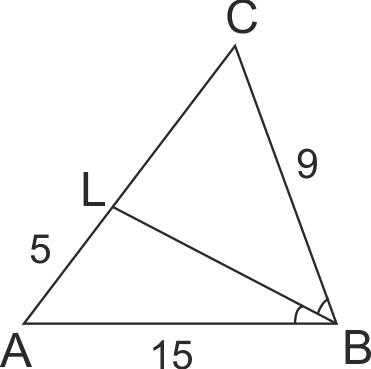
В ΔABC AB = 15, BC = 9. BL е ъглополовяща на ∠ABC (L∈AC), като AL = 5. Страната AC на ΔABC е равна на:
8
11
12
3
-
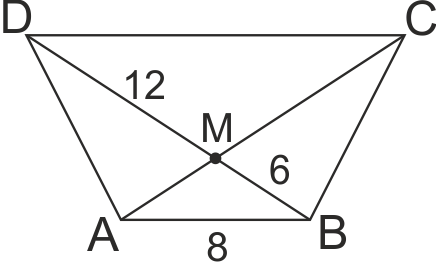
В трапец ABCD (AB || CD, AB<CD ) ACxDB = M така, че DM = 12, BM = 6 и AB = 8.Основата CD е равна на:
4
16
24
10
-
Точка M е медицентър на ΔABC. Права през точка M успоредна на BC пресича АC и AB в точки P и Q. SCPQ = 20, то SABC е равно на:
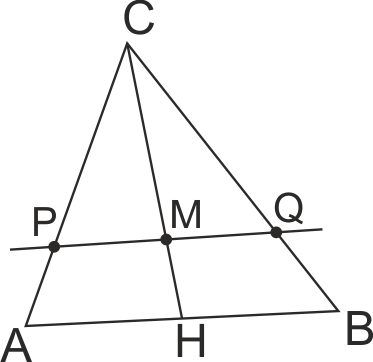
30
друг отговор
45
80
-
Периметърът на ΔABC е 50. CL е ъглополовяща на ∠ACB (L ∈ AB), като AL = 4, BL = 6. Страните AC и BC имат дължини:
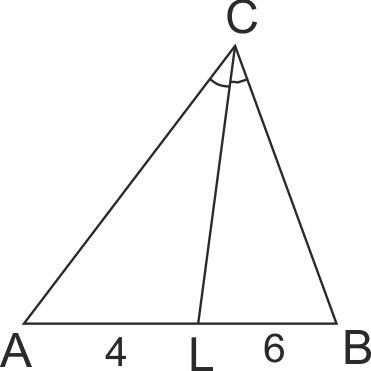
10 и 24
16 и 10
20 и 30
16 и 24
-
За ΔABC ∠ACB = 900 и SABC = 116, катетите му се отнасят както 3:7. Височината към AB разделя ΔABC на два триъгълника. Лицата на тези триъгълници са равни на:
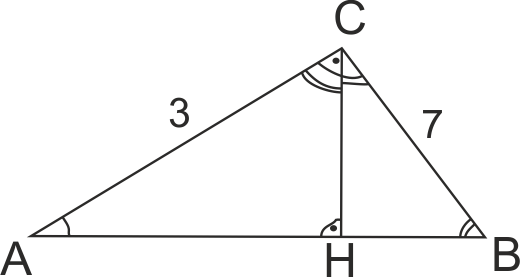
34,8 и 81,2
18 и 98
52 и 64
друг отговор
-
ΔABC ~ ΔMNP AB = 12, a MN = 16. Ъглополовящите на ∠BAC към ∠NMP се отнасят така както:
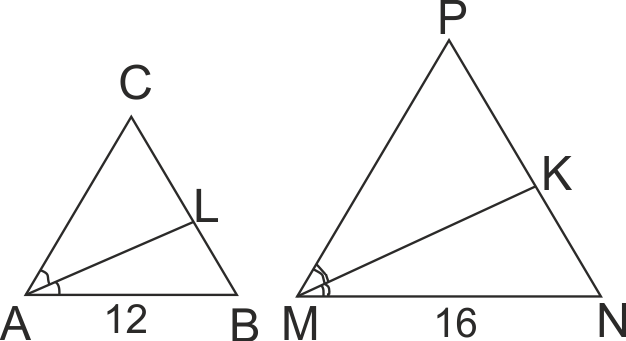
3/4
3/4 или 4/3
4/3
2:1
-
Катетът и хипотенузата на един правоъгълен триъгълник са съответно 3 см и 5 см, а на друг правоъгълен триъгълник - 6 см и 11 см. Подобни ли са двата триъгълника?
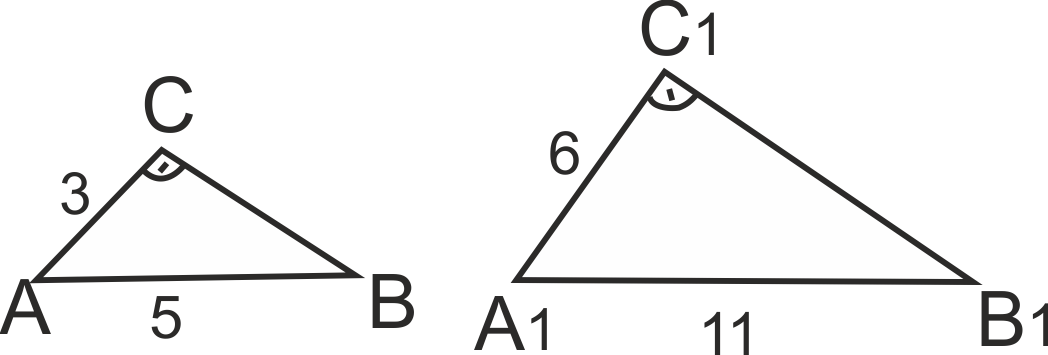
Да
Възможно
НЕ
Не съм сигурен
-
Страните на един триъгълник са 6 см, 12 см и 10 см, а на друг - 18 см, 36 см и 30 см. Подобни ли са двата триъгълника?
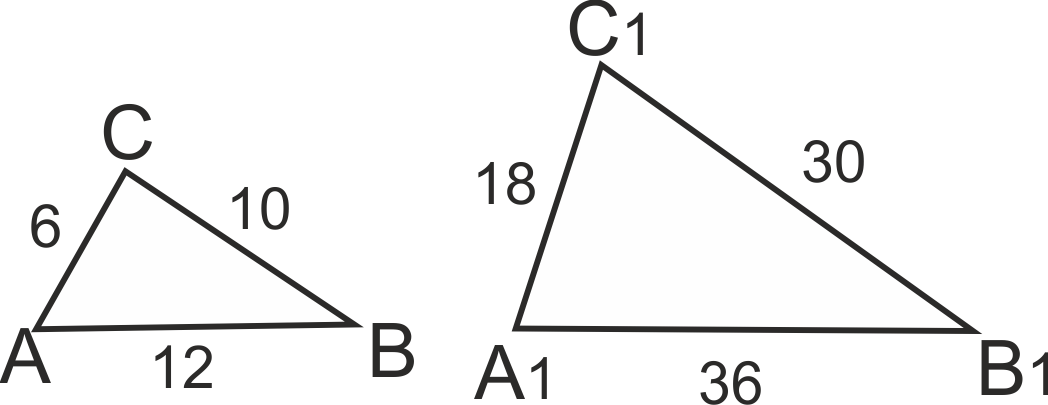
Да
Не съм сигурен
Възможно
Не