<<<  1  2  3  4  5  6  7  8  9  10  11  >>>

---

Признаци:

III признак:

Доказателство: Нека за ΔABC и ΔA₁B₁C₁ е изпълнено AB/A₁B₁ = AC/A₁C₁ = BC/B₁C₁.

Нанасяме A₁B₁ върху лъча AB^→ до точката B₂ (фиг.5). Нека правата m през B₂, успоредна на BC, пресича AC в точка C₂.

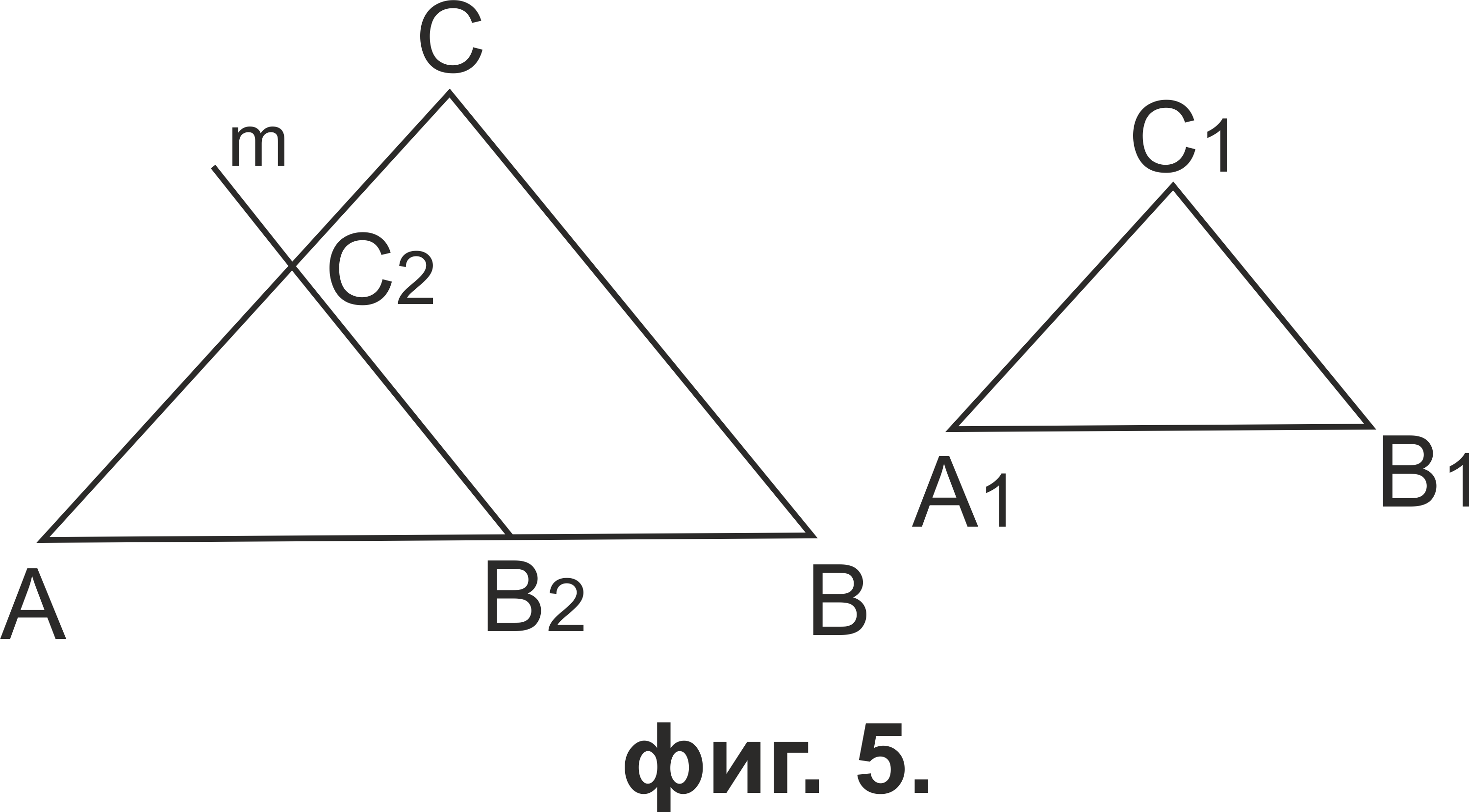
От лемаа за пропорционалните отсечки в триъгълника имаме AB/A₂B₂ = AC/A₂C₂ = BC/B₂C₂. От A₁B₁ = AB₂ получаваме AB/A₁B₁ = AB/AB₂ = AC/AC₂ = BC/B₂C₂. Като вземем предвид, че AB/A₁B₁ = AC/A₁C₁ = BC/B₁C₁, откъдето AC/AC₂ = AC/A₁C₁ и BC/B₂C₂ = BC/B₁C₁. Следователно AC₂ = A₁C₁ и B₂C₂ = B₁C₁. Тогава ΔA₁B₁C₁ ≅ ΔАB₂C₂ по трети признак за еднаквост, т.е. ∠B₂AC₂ = ∠B₁A₁C₁ и ∠AB₂C₂ = ∠A₁B₁C₁. Но ∠B₂AC₂ = ∠BAC и ∠AB₂C₂ = ∠ABC (m||BC). Следователно ∠BAC = ∠B₁A₁C₁, ∠ABC = ∠A₁B₁C₁ и триъгълниьците ABC и A₁B₁C₁ са подобни по първи признак за подобност.

---

<<<  1  2  3  4  5  6  7  8  9  10  11  >>>