Подобни триъгълници

<<< 1 2 3 4 5 6 7 8 9 10 11 >>>

Лица на подобни многоъгълници

Всяка фигура има определено лице, което е положително число. Основните свойства на лицата на фигурите са:

Еднаквите фигури имат равни лица.
Ако една фигура е разделена на части, то лицето на фигурата е равно на сбора от лицата на частите.
Лицето на правоъгълник с дължини на страните a и b е ab.

Като използваме тези свойства, ще изведем формулите за пресмятане на лицата на някои многоъгълници.

Лице на триъгълник. Лицето S на триъгъник със страна c и височина към нея h_c е S=1/2ch_c.

Лице на успоредник - Лицето S на успоредник със страна a и b височини към тях h_a и h_b е S=ah_a=bh_b.

Лице на трапец. Лицето S на трапец ABCD с основи AB=a и CD=b и височина h е S=(a+b)*h/2.

Теорема 1. Лицето S на многоъгълник с периметър 2p, описан около окръжност с радиус r, е S=pr.

Доказателство. Нека многоъгълникът A₁A₂...A_n е описан около окръжност k с центер O и радиус r, която се допира до страните му в точки H₁, H₂,..., H_n (фиг.9).

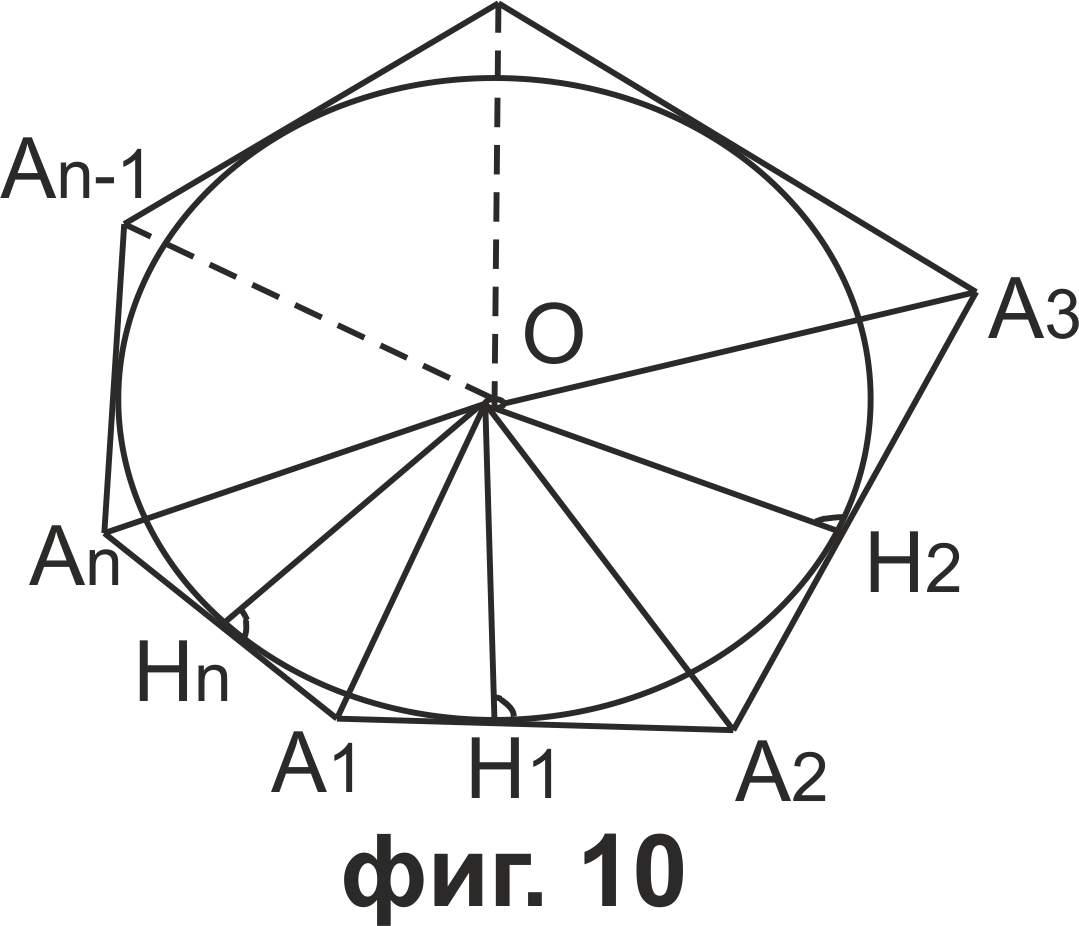
Тогава OH₁⊥A₁A₂, OH₂⊥A₂A₃,..., OH_n⊥A_nA₁. Лицето S на многоъгълника е равно на сбора от лицата на триъгълниците OA₁A₂, OA₂A₃,..., OA_nA₁. Следователно S=1/2A₁A₂*OH₁+1/2A₂A₃*OH₂+...+1/2A_nA₁*OH_n. Тъй като OH₁=OH₂=...OH_n=r, то S=1/2A₁A₂*r+1/2A₂A₃*r+...+1/2A_nA₁*r=1/2(A₁A₂+A₂A₃+...+A_nA₁)*r. Но A₁A₂+A₂A₃+...+A_nA₁=2p, откъдето S=pr.

Тъй като във всеки триъгълник може да се впише окръжност, то

Лицето S на триъгълник може да се пресмята по формулата S=pr.

Теорема 2. Отношението на лицата на два подобни триъгълника е равно на квадрата на коефициента на подобност.

Доказателство. Нека ΔABC ~ ΔA₁B₁C₁ и AB : A₁B₁=k (фиг.10).

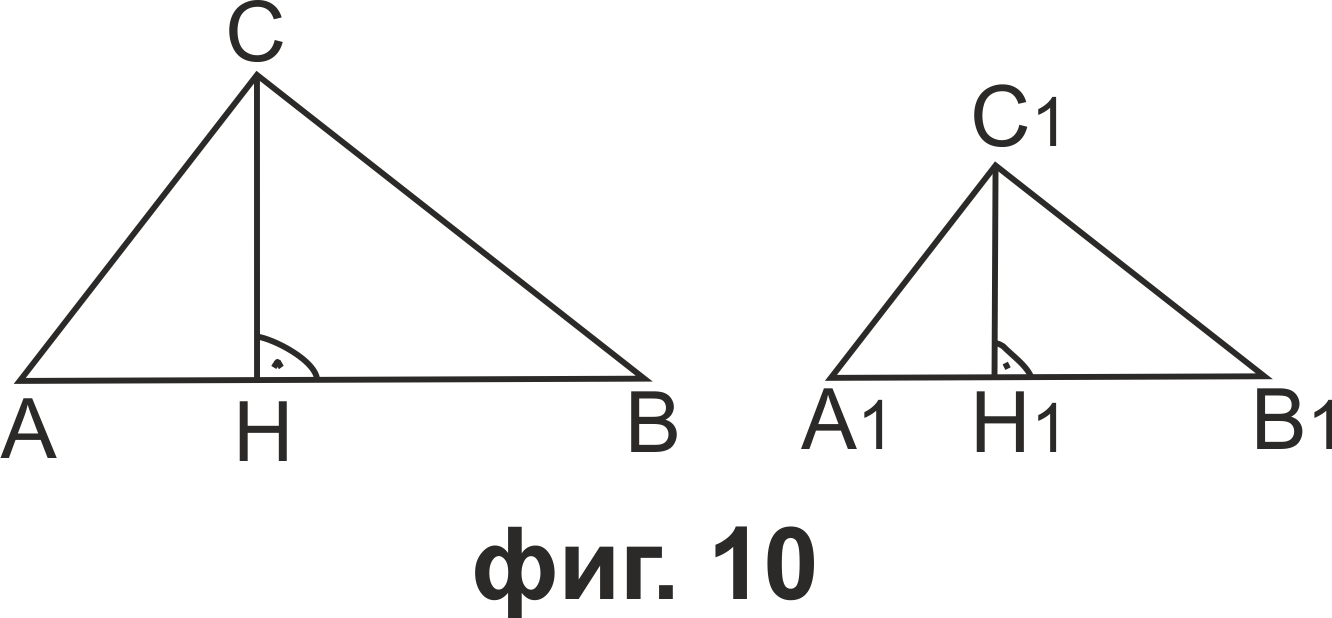
Ако CH и C₁H₁ са височините съответно към АB и A₁B₁, то CH/C₁H₁=AB/A₁B₁=k. Тогава AB=kA₁B₁ и CH=kC₁H₁. Оттук за отношението на лицата на триъгълниците ABC и A₁B₁C₁ имаме S/S₁ = S_ABC/S_A₁B₁C₁ = 1/2AB*CH/1/2A₁B₁*C₁H₁ = 1/2kA₁B₁*C₁H₁/1/2A₁B₁*C₁H₁ = k².
Следователно S=k²S₁, с което теоремата е доказана.
Същата зависимост съществуваи между лицата на два подобни многоъгълника.

Теорема 3. Отношението на лицата на два подобни многоъгълника е равно на квадрата на коефициента на подобност.

Доказателство. Нека подобността φ с коефициент k изобразява многоъгълника A₁А₂...А_n с лице S_A в многоъгълника B₁B₂...B_n с лице S_B (на фиг.11 n=6).

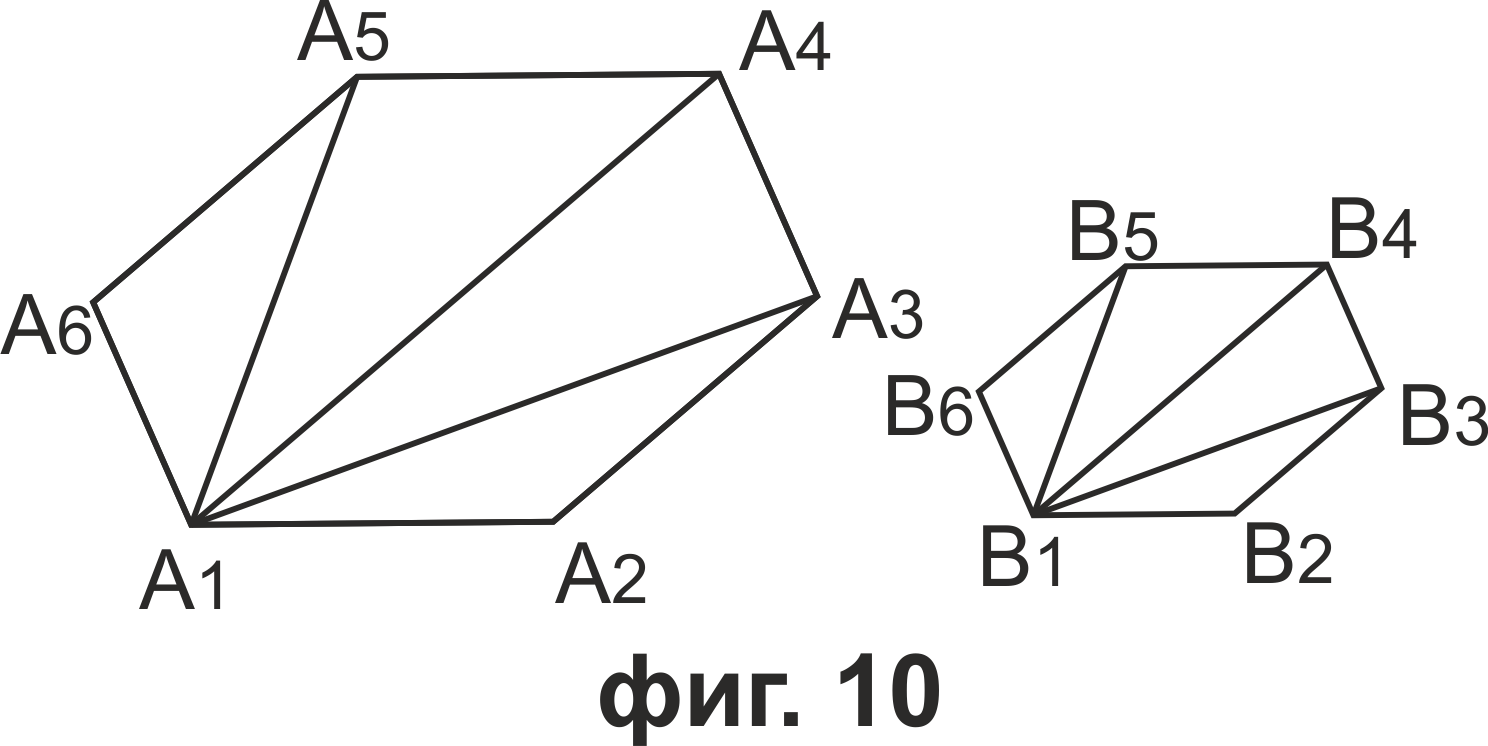
Нека многоъгълниците са разделени на триъгълници A₁A₂A₃, A₁A₃A₄, ..., A₁A_n-1A_n и B₁B₂B₃, B₁B₃B₄, ..., B₁B_n-1B_n. Тъй като ΔA₁A₂A₃ ~ ΔB₁B₂B₃, ΔA₁A₃A₄ ~ ΔB₁B₃B₄, ..., ΔA₁A_n-1A_n ~ ΔB₁B_n-1B_n (като съответни при подобността φ), то съгласно теорема 2: S_B₁B₂B₃ = k²*S_A₁A₂A₃, S_B₁B₃B₄ = k²*S_A₁A₃A₄, ..., S_{B₁B_n-1B_n} = k²*S_{A₁A_n-1A_n}. Но S_A = S_A₁A₂A₃ + S_A₁A₃A₄ +...+ S_{A₁A_n-1A_n} и S_B = S_B₁B₂B₃ + S_B₁B₃B₄ +...+ S_{B₁B_n-1B_n} = k²(S_A₁A₂A₃ + S_A₁A₃A₄ +...+ S_{A₁A_n-1A_n}). Следователно S_B = k²*S_A.

<<< 1 2 3 4 5 6 7 8 9 10 11 >>>

Меню