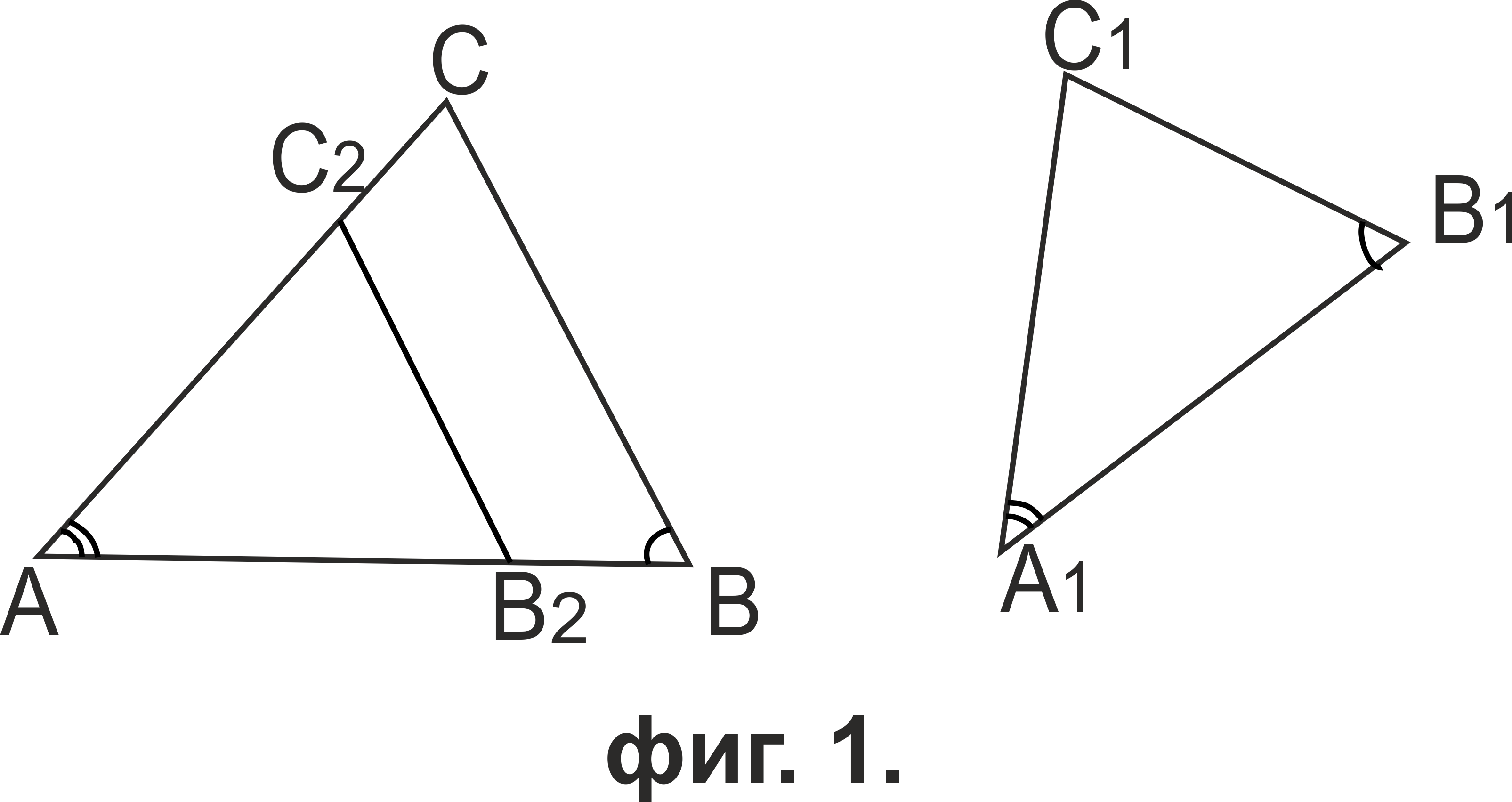
Тъй като сборът от ъглите в триъгълник е 180°, то ∠ACB=∠A1C1B1. Следователно, за да установим, че страните им са пропорционални, т.е. AB/A1B1=AC/A1C1=BC/B1C1.
Нанасяме страната A1B1 върху лъча AB→ до точката B2. Нека правата m, през точка B2, успоредна на BC, пресича AC в точка C2. Тъй като BC||B2C2, то ∠АB2C2=∠ABC=∠A1B1C1. Тогава ΔАB2C2≅ΔA1B1C1. От лемата за пропорционалните отсечки в триъгълника получаваме AB/AB2=AC/AC2=BC/B2C2.
Тъй като AB2=A1B1, AC2=A1C1, то AB/A1B1=AC/A1C1=BC/B1C1. Следователно ΔABC~ΔA1B1C1.
С помощта на доказаната теорема лесно се получават следните важни следствия:
Наистина, ако ΔABC~ΔA1B1C1, a CH и C1H1 са съответни височини, то
∠AHC=∠A1H1C1=90°
∠CAH=∠C1A1H1 (фиг.2), откъдето по
първи признак за подобност ΔAHC~ΔA1H1C1.
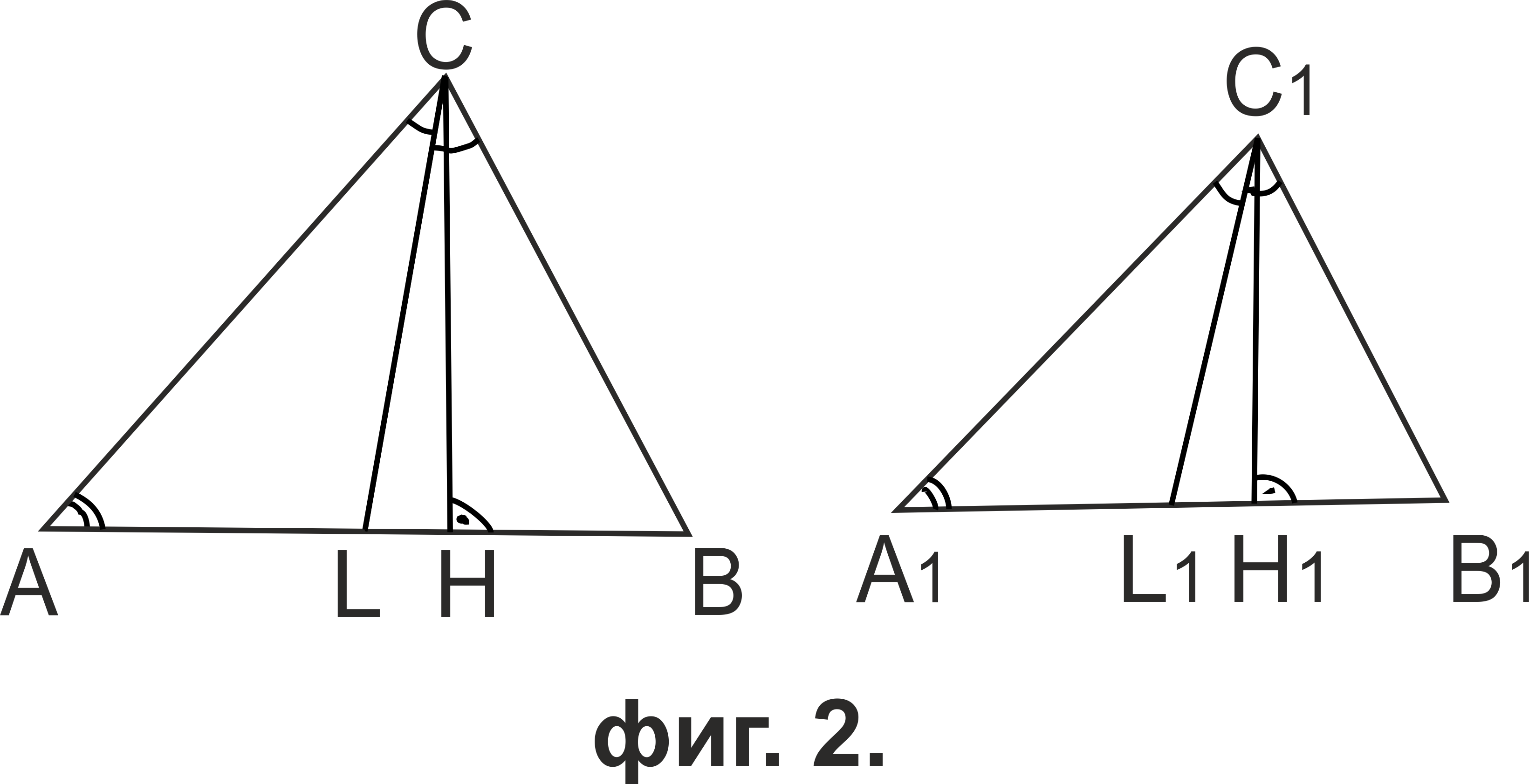
Следователно CH : C1H1=AC : A1C1. Аналогично за ъглополовящите CL и C1L1 имаме ∠ACL=∠A1C1L1 така, че ΔACL~ΔA1C1L1 (фиг.2), откъдето следва CL : C1=AC : A1C1.
Ako ΔABC~ΔA1B1C1 =>
a/a1=b/b1=c/c1=ha/ha1=lb/lb1=mc/mc1=P/P1
=R/R1=r/r1=k.
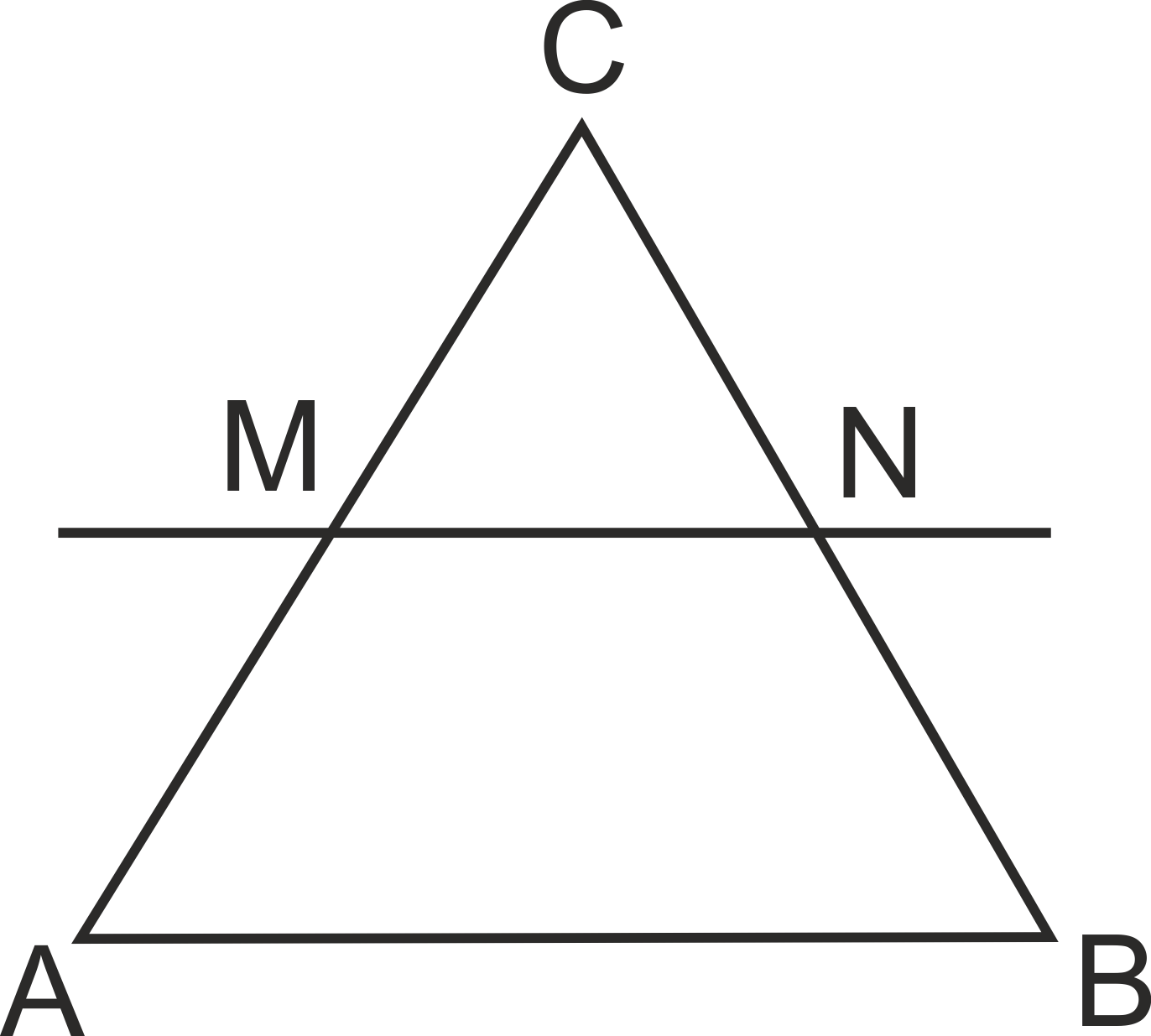
Ако в произволен триъгълник ABC ще построим права MN||AB, то получения триъгълник MNC е подобен на триъгълника ABC по I признак.
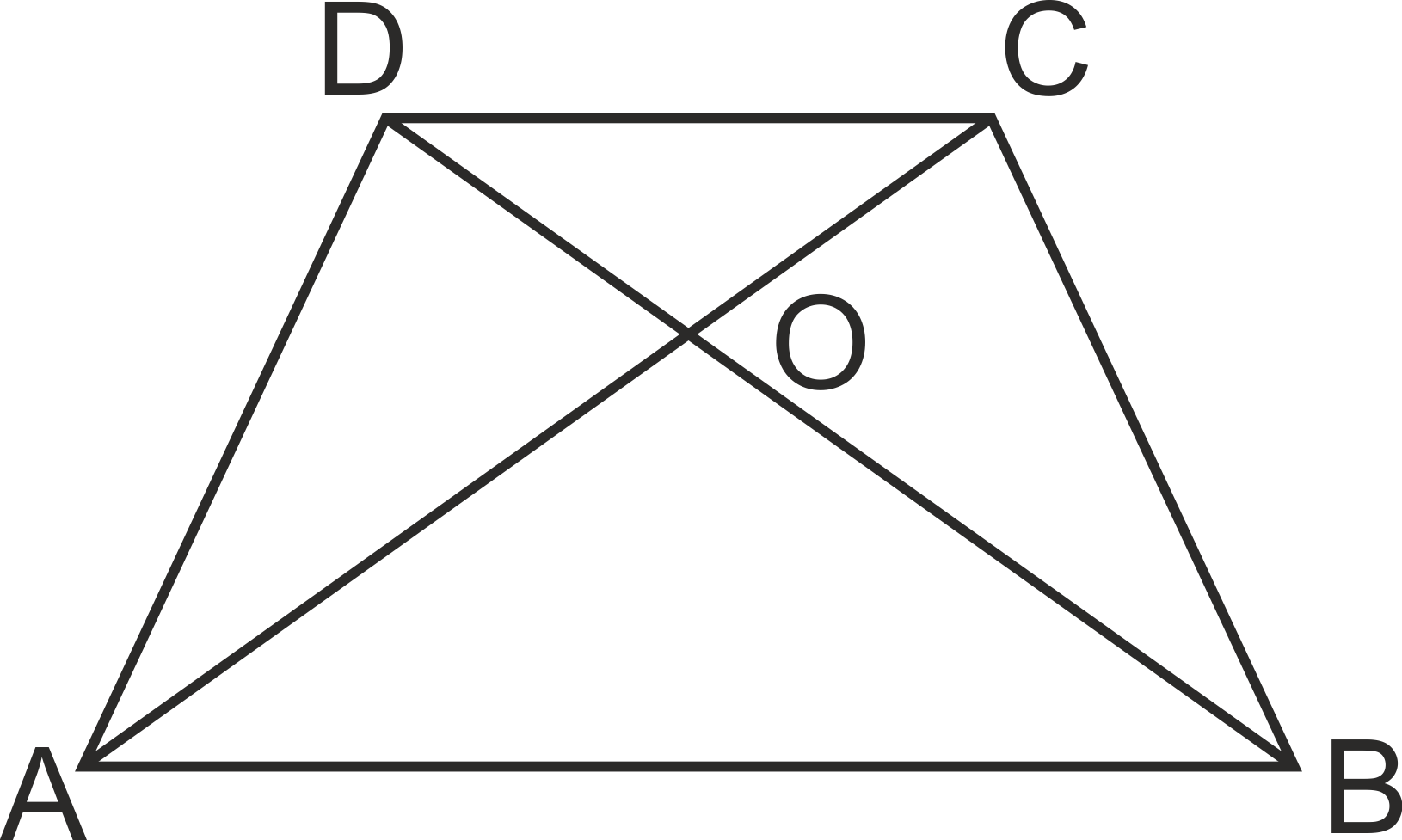
Ако в произволен трапец ABCD ще построим диагонали AC и BD, където ACxBD=O, то получените триъгълниците AOB и COD са подобни по I признак.
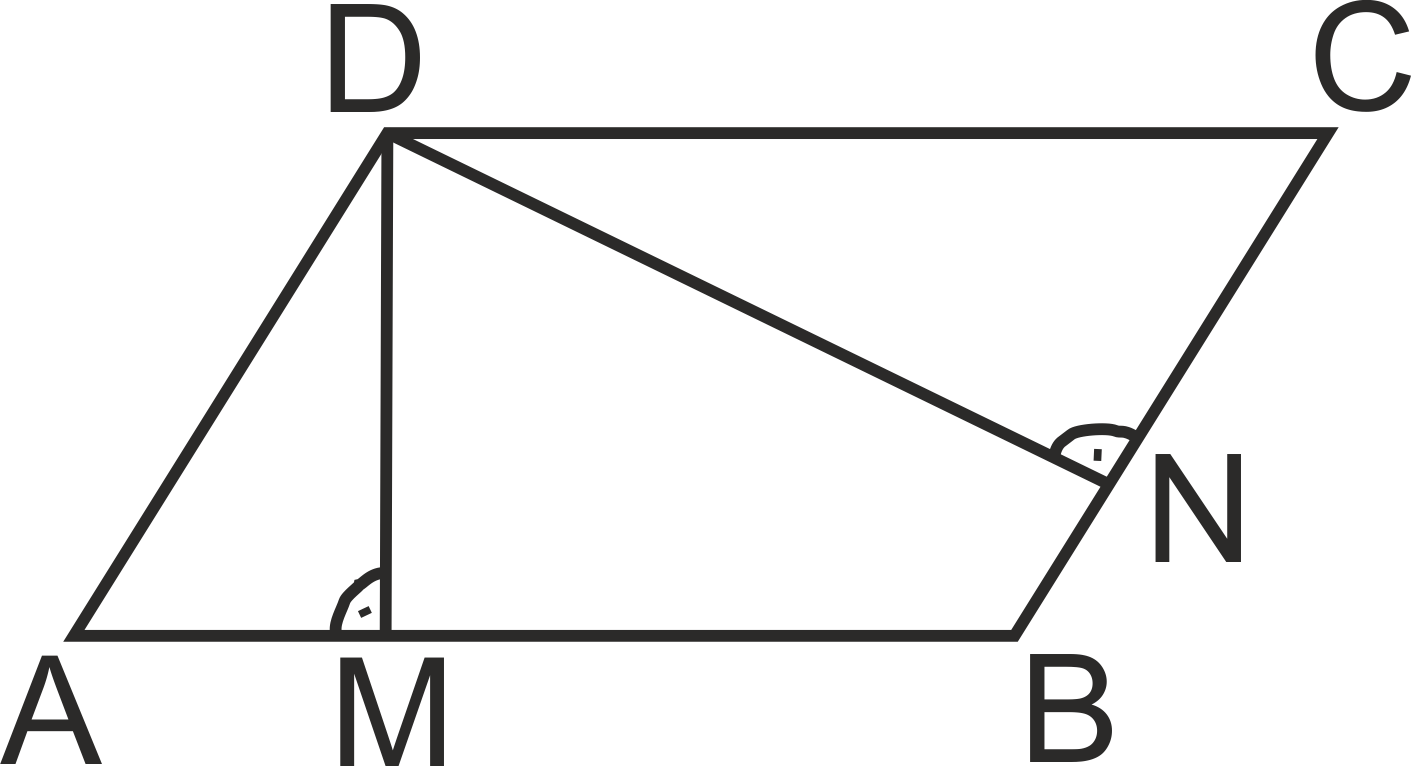
Ако в произволен успоредник ABCD ще построим височини през точка D към страни AB и BC, то получените триъгълници AMD и CND са подобни по I признак.

Ако в правоъгълен триъгълник ABC ще построим височина CH, то ΔABC~ΔACH и ΔABC~ΔBCH => ΔACH~ΔBCH по I признак.
=> метрични зависимости в правоъгълен триъгълник
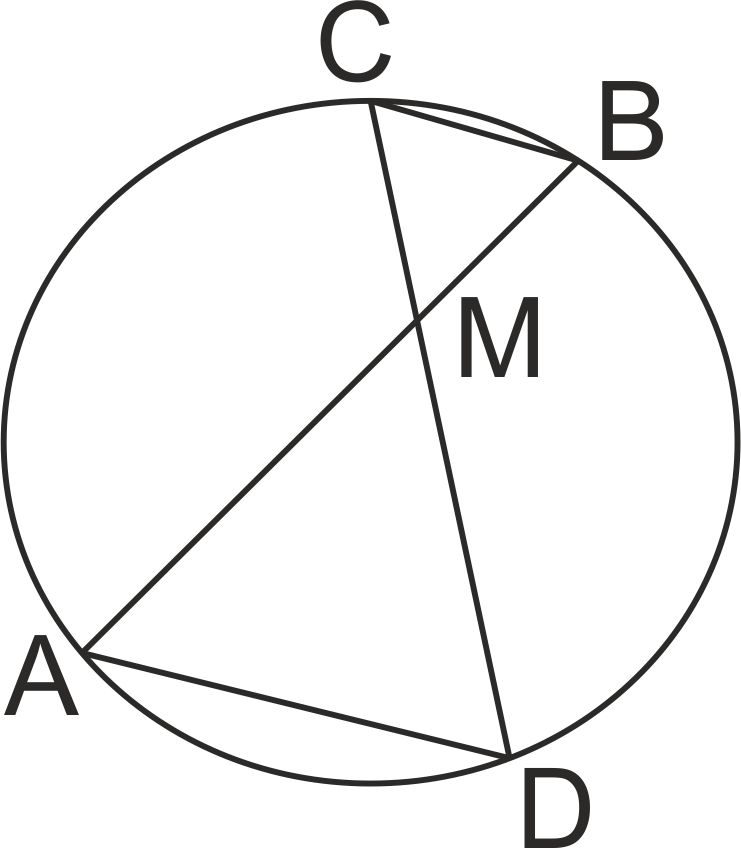
В окръжност
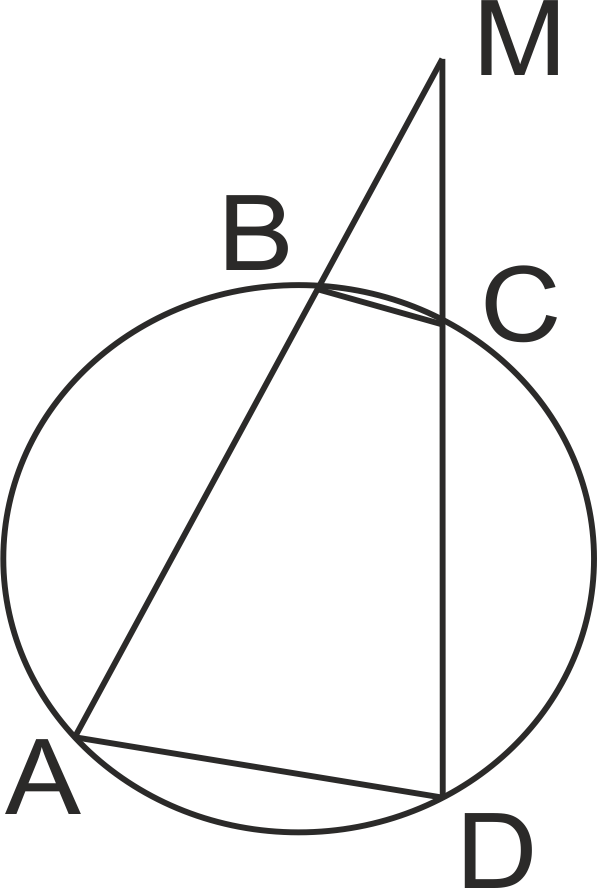
В окръжност
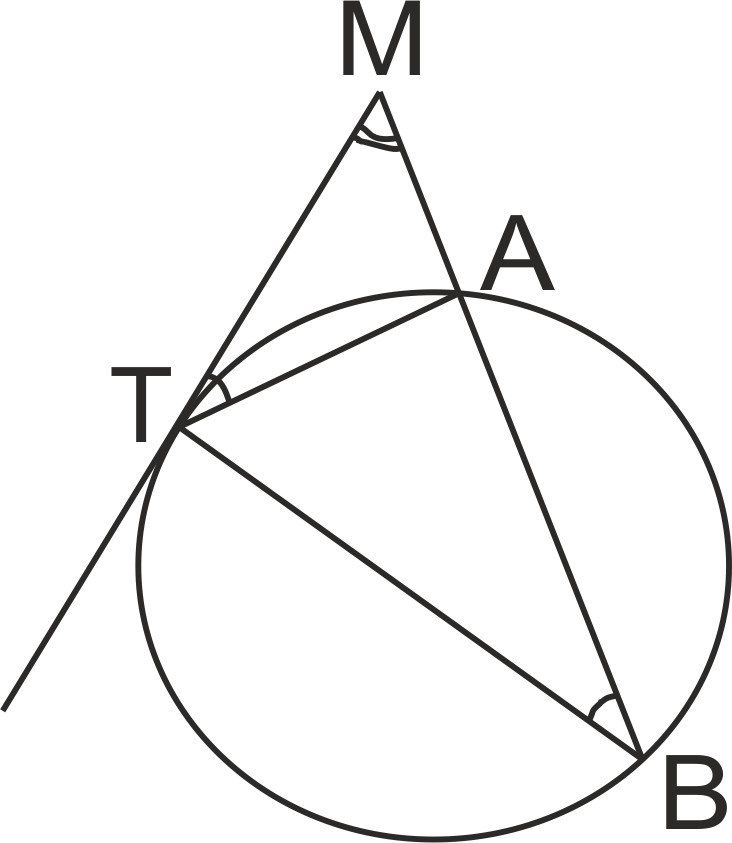
В окръжност