Признаци:

IV признак:

Доказателство: Нека за правоъгълните триъгълниците ABC и A₁B₁C₁ с прави ъгли при върховете C и C₁ е изпълнено AB/A₁B₁ = AC/A₁C₁.

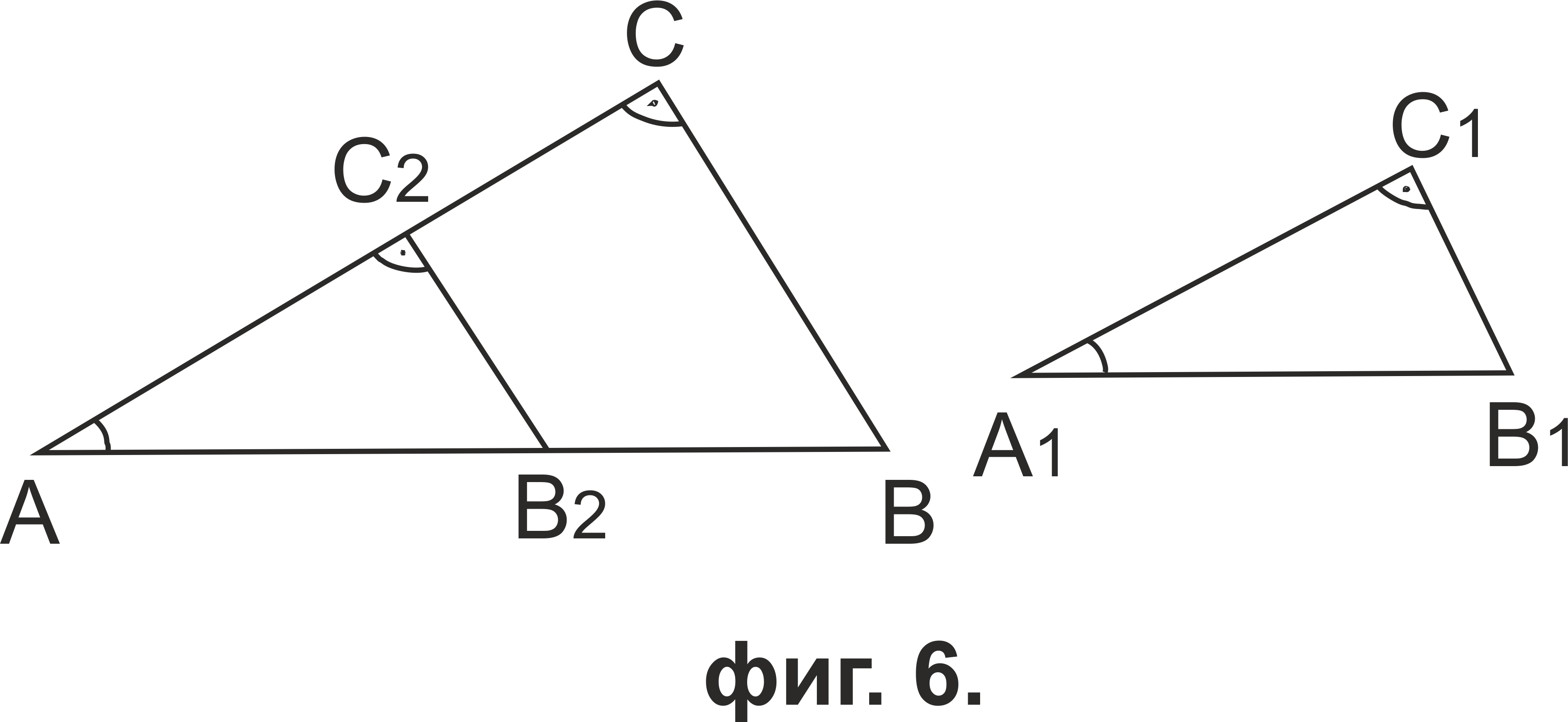
Нанасяме катета A₁C₁ върху лъча AC^→ до точката C₂ (Фиг.6). Правата през C₂, перпендикулярна на AC, пресича AB в точка В₂. Тъй като C₂B₂||BC, то от теорвмата на Талес следва, че AB/AB₂ = AC/AC₂, и като вземем предвид условието, получаваме AB₂ = AB и AC₂ = AC. Тогава по признака за еднаквост на правоъгълни триъгълници ΔAB₂C₂ ≅ ΔA₁B₁C₁. Следователно ∠B₂AC₂ = ∠B₁A₁C₁ = ∠BAC, откъдето заключаваме, че триъгълниците ABC и A₁B₁C₁ са подобни по първи признак.