(1)
(2)
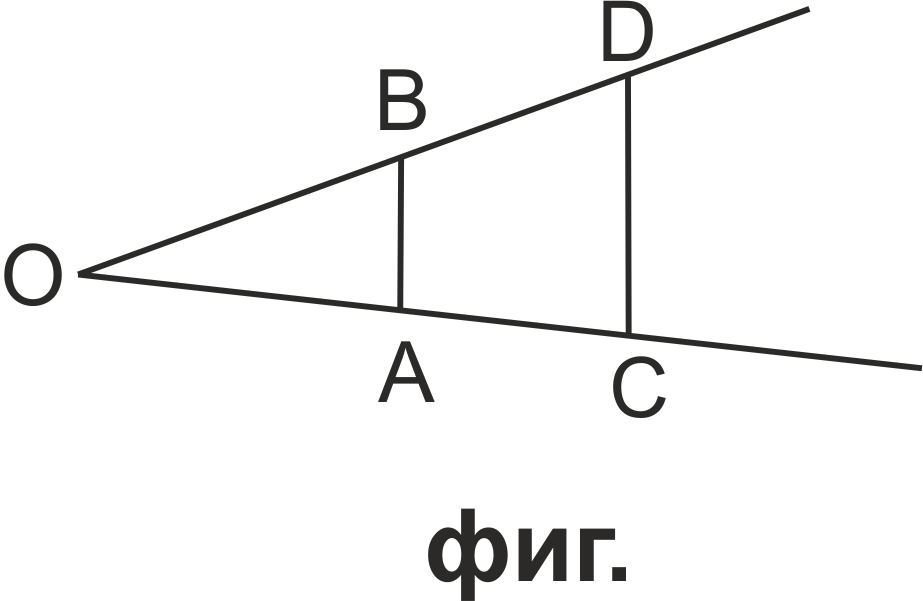
От фиг. => OD = OB + BD; OC = OA + AC;
От (1) => (OB + BD)
AB

От фиг. => OD = OB + BD; OC = OA + AC;
От (1) => (OB + BD)
AB