Подобни триъгълници

<<< 1 2 3 4 5 6 7 8 9 10 11 >>>

Подобност. Подобни фигури

Определение. Геометрично преобразувание, при което за всеки две точки M, N и техните образи M₁, N₁ е изпълнено равенството M₁N₁=kMN (k - положително число), се нарича подобност с коефициент k.

От определение за подобност следва, че:

Подобнст с коефициент k=1 е еднаквост.

Теорема 1. Образът на отсечка при подобност е отсечка.

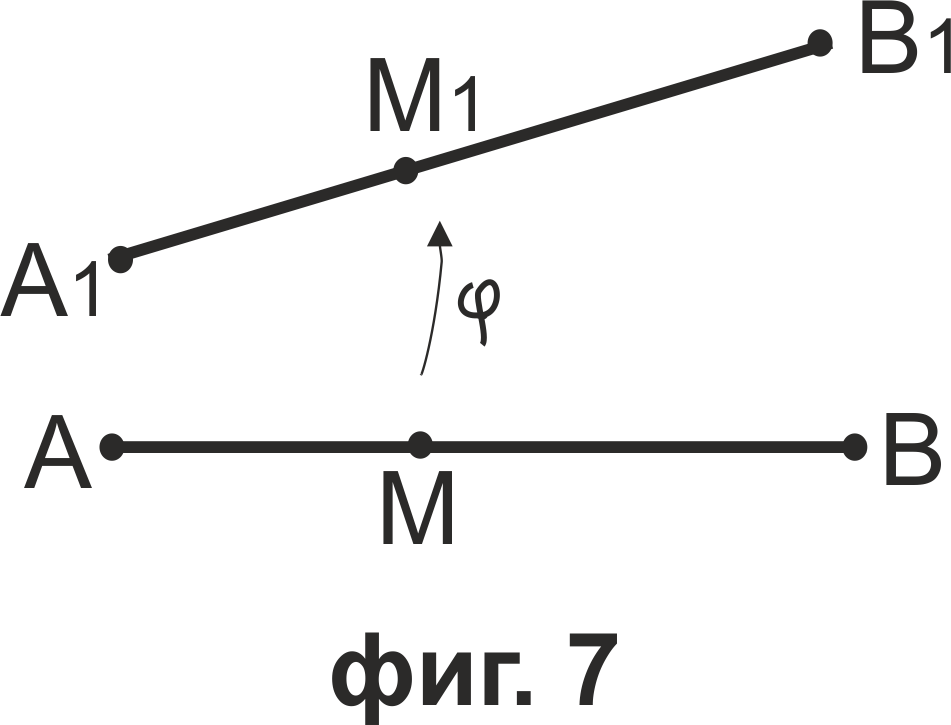
При подобност среда на отсечка се изобразява в средата на образа й.

От теорема 1 непосредствено следва, че при подобност:

образът на лъч е лъч;
образът на права е права;
образът на ъгъл е ъгъл.

Теорема 2. При подобност ъгъл се изобразява в равен на него ъгъл.

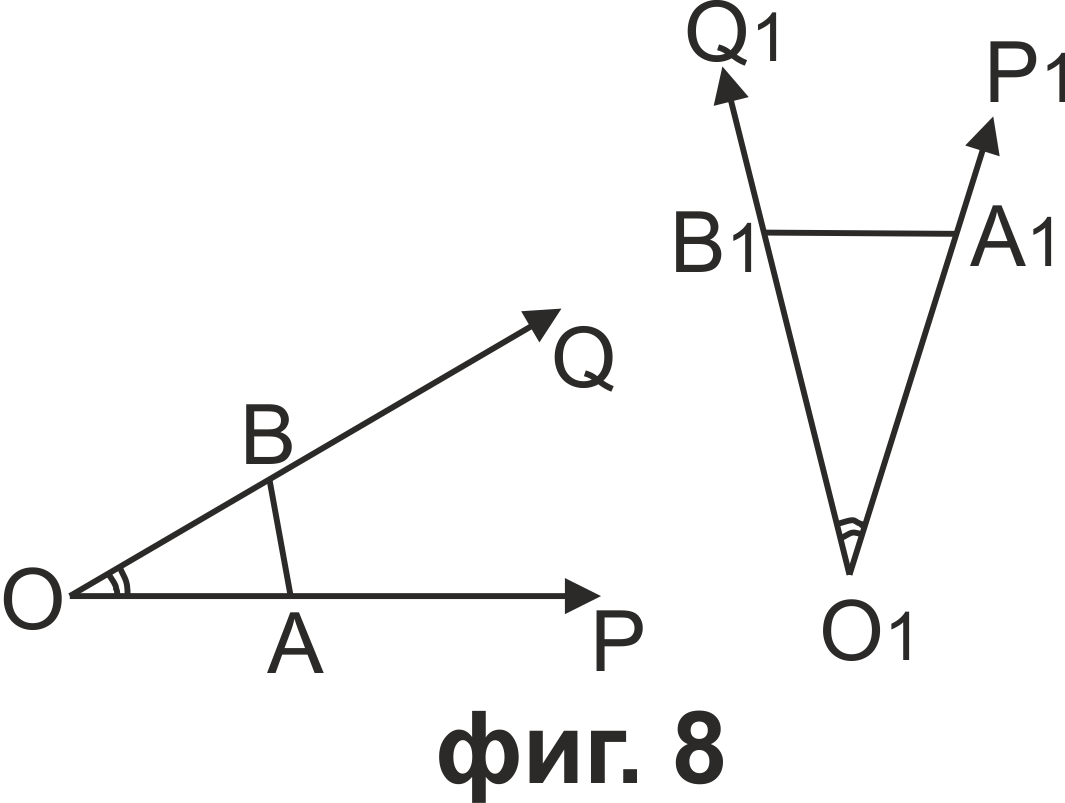
Ако два триъгълника са съответни при подобност, то те са подобни.
     Вярно е и обратно твърдение:
    Ако два триъгълника са подобни, то съществува подобност, която изобразява единия в другия.
    Като използваме понятието подобност, можем да дадем общо определение за подобни фигури.

Определение. Две фигури се наричат подобни, когато са съответни при подобност.

Ако фигурата F е подобна на фигурата F₁, накратко пишем F~F₁.

Като се използват свойствата на подобностите, може да се каже, че два многоъгълника са подобни тогава и само тогава, когато съответните им ъгли са равни и съответните страни пропорционални.

<<< 1 2 3 4 5 6 7 8 9 10 11 >>>

Меню