Tриъгълникът е напълно определен с три елемента, от които поне един е линеен. Линейният елемент, обуславя големината на триъгълника. Следователно, ако пренебрегнем линейният елемент, а вземем пред вид ъглите или отношенията на страните, можем да построим безбройно много триъгълници, различни по големина, но с една и съща форма. Това дава възможност да формулираме, следното определение за подобни триъгълници:
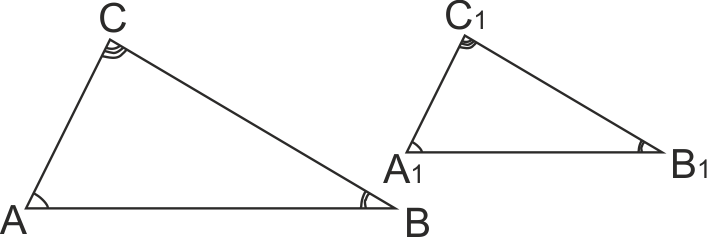
Ако ΔАВС ~ ΔА1В1С1 то ∠ABC=∠A1B1C1, ∠ACB=∠A1C1B1, ∠CAB=∠C1A1B1 и АВ/А1В1=ВС/В1С1=СА/С1А1=k, числото k се нарича коефициент на подобност (коефициент на подобие) за триъгълниците АВС и А1В1С1.
Символът, означаващ подобност на фигури, не е нищо друго освен легнала латинската буква
Ако два триъгълника АВС и А1В1С1 са еднакви, те са подобни с коефициент на подобие 1. Наистина ъглите на тези триъгълници са съответно равни, а за страните са изпълнени равенствата АВ/А1В1=ВС/В1С1=СА/С1А1=1.
Подобните триъгълници притежават и следните свойства:
1. ΔАВС~ΔАВС (рефлективност);
2. Ако ΔАВС~ΔА1В1С1, то ΔА1В1С1~ΔАВС (симетричност);
3. Ако ΔАВС~ΔА1В1С1 и ΔА1В1С1~Δ
А2В2С2 то ΔАВС~ΔА2В2С2
(транзитивност).