<<<  1  2  3  4  5  6  7  8  9  10  11  >>>

---

Признаци:

II признак:

Доказателство: Нека за ΔABC и ΔA₁B₁C₁ е изпълнено ∠BAC = ∠B₁A₁C₁ и AB/A₁B₁ = AC/A₁C₁.

За да докажем, че триъгълниците са подобни, съгласно пръви признак за подобност е достатъчнода докажем, че ∠ABC = ∠A₁B₁C₁.

Както и при доказателство на първи признак за подобност на предишната страница, построяваме ΔАB₂C₂ по следния начин: нанасяме A₁B₁ върху лъча AB^→ до точката B₂ и A₁C₁ - върху лъча AC^→ до точката C₂ (фиг.3).

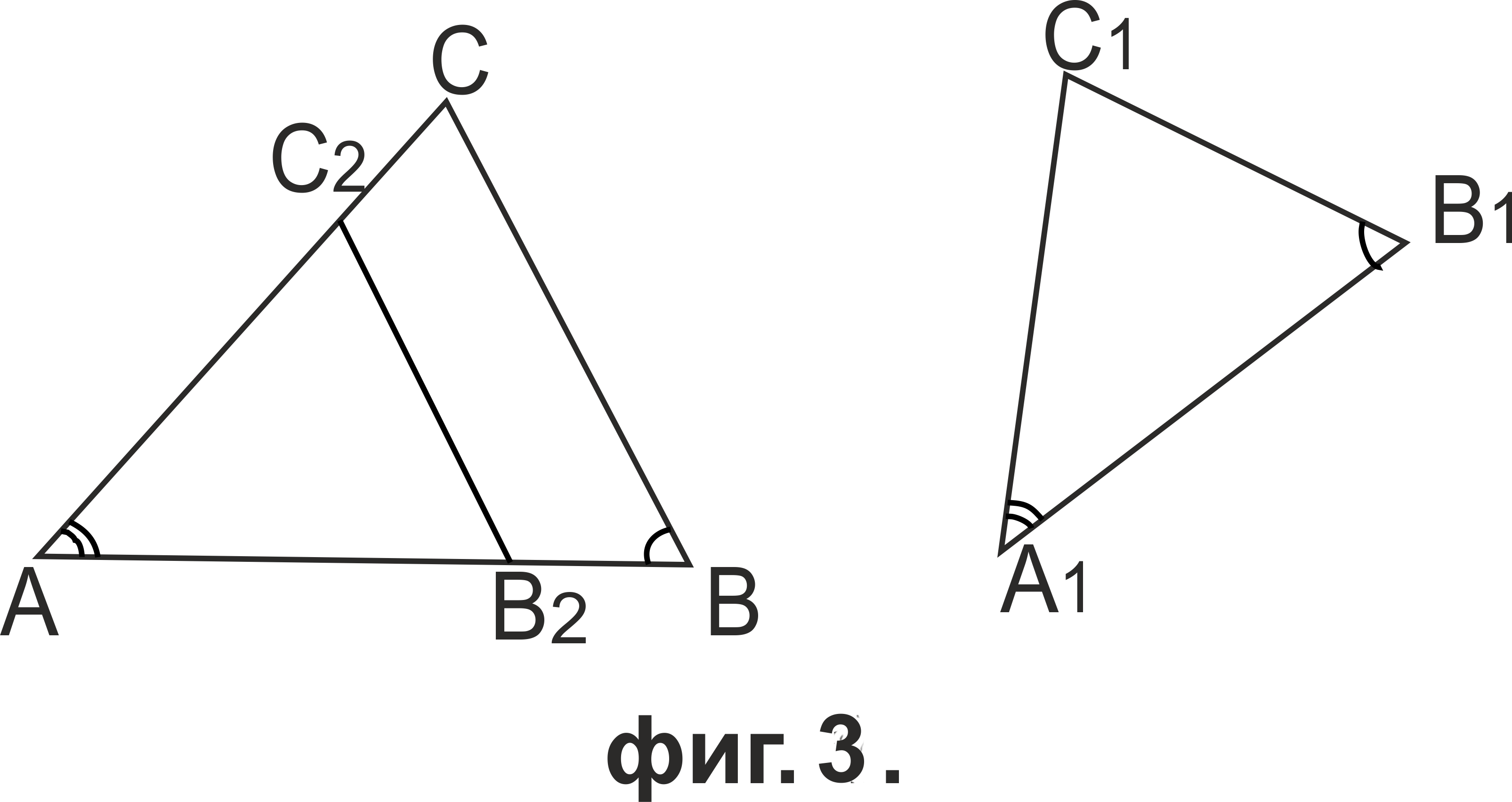
Тогава ΔАB₂C₂ ≅ ΔA₁B₁C₁ са еднакви по първи признак и ∠АB₂C₂ = ∠A₁B₁C₁.

От условието AB/A₁B₁ = AC/A₁C₁ получаваме AB/AB₂ = AC/AC₂ => B₂C₂||BC, откъдето ∠АB₂C₂ = ∠ABC. Следователно ∠ABC = ∠A₁B₁C₁, с което доказахме, че ΔABC ~ ΔA₁B₁C₁.

От втори признак за подобност на триъгълници получаваме следното важно следствие:

Нека ΔABC ~ ΔA₁B₁C₁ и M и M₁ са средите на страните AB и A₁B₁ (фиг.4).

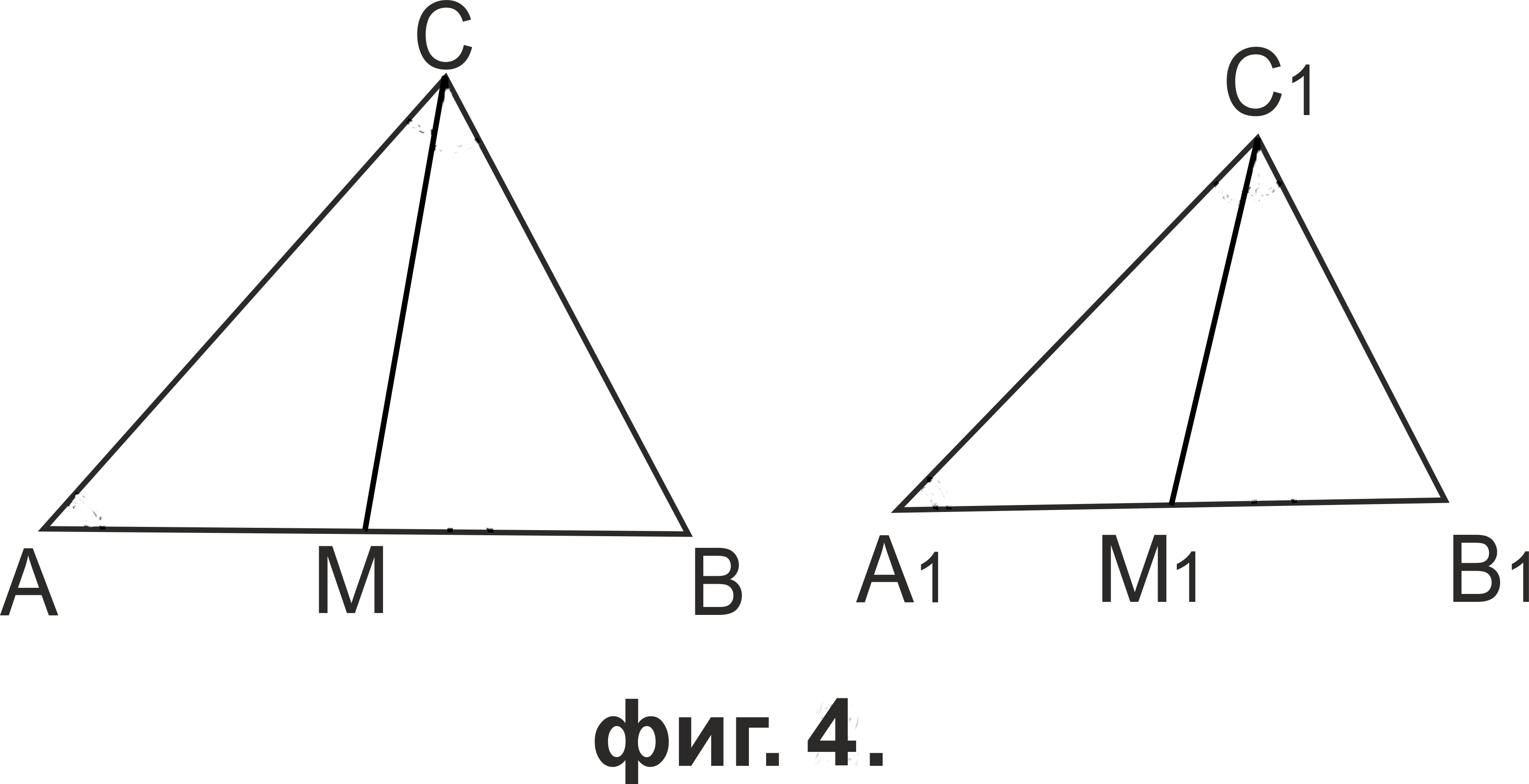
За да докажем, че CM : C₁M₁ = AC : A₁C₁, е достатъчно да намерим два подобни триъгълника със съответни страни AC и A₁C₁, и CM и C₁M₁. Да разгледаме ΔACM и ΔA₁C₁M₁. От ΔABC ~ ΔA₁B₁C₁ имаме ∠MAC = ∠M₁A₁C₁ и AB/A₁B₁ = AC/A₁C₁. Тъй като AB = 2AM и A₁B₁ = 2A₁M₁, то AM/A₁M₁ = AC/A₁C₁. Следователно по втори признак за подобност на триъгълници ΔAMC ~ ΔA₁M₁C₁, от където получаваме CM : C₁M₁ = AC : A₁C₁.

---

<<<  1  2  3  4  5  6  7  8  9  10  11  >>>