<<< 1
2 3 4
5 >>>
Задача 21.
ΔABC AC = BC = 60. Центърът на вписаната окръжност дели височината към основата в отношение 12 : 5, считано от
върха на триъгълника. Намерете основата на ΔABC.
Центъра на вписана окръжност в триъгълника е пресечна точка на ъглополовящите в триъгълника.
Приложете свойсвото на ъглополовяща.
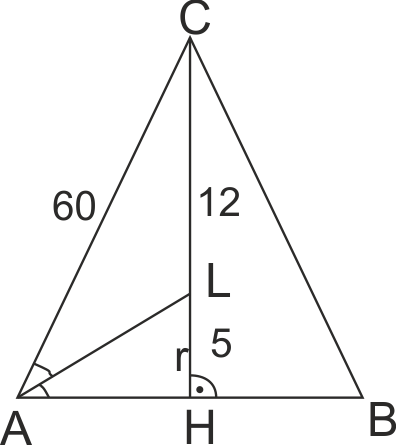
В равнобедрен триъгълник AB = AH + HB = 2AH.
От пропорцията LH/LC = AH/AC => AH = (5*60)/12 => AH = 25.
AB = 2AH = 2*25 = 50. AB = 50.
Задача 22.
Даден е ΔABC със страни AB = c и AC = b. Построена е ъглополоващата AL (L ∈ BC) и през точка L е построена
права LP (P ∈ AB) и LP || AC. Намерете отношението на SΔLPB : SΔABC
Използвайте свойството на ъглополовящата. Приложете 2 теорема от раздела "Теория" от подраздела "Лица на подобни многоъгълници".
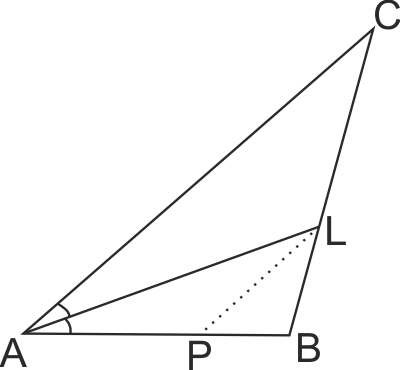
AL - ъглополовяща на ∠A => CL/BL = AC/AB => CL/BL = b/c => CL = (b/c)*BL;
ΔABC ~ ΔPBL (по I признак) защото ∠B - общ, ∠LPB = ∠CAB (като съответни ъгли на AC || PL);
BC = CL + BL = (b/c)*BL + BL = (b + c)/c*BL;
От ΔABC ~ ΔPBL =>
SΔLPB/SΔABC = (c/(b + c))2 = c2/(b2 + 2bc + c2).
Задача 23.
Нека точка M, точка N и точка P са среди съответно настраните AC, BC и AB на ΔABC.
АКо ΔABC е с лице S да се намери:
а) лицето на ΔMNC;
б) лицето на ΔMNP.
Използвайте свойството на лицата на подобни триъгълници.
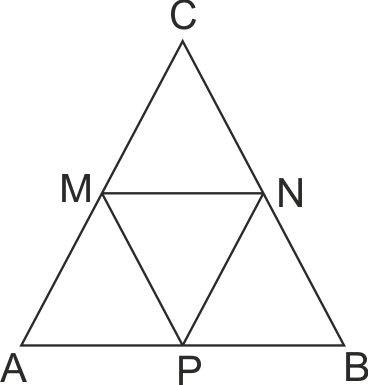
а) Точки M и N са среди на AC и BC => CM = 1/2AC => CM/AC = 1/2;
CN = 1/2BC => CN/BC = 1/2.
ΔMNC ~ ΔABC (по II признак, защото ∠C - общ, CM/AC = CN/BC = 1/2 ).
От свойството на лицата: SΔMNC/SΔABC = (CN/BC)2 = (1/2)2 = 1/4 => SΔMNC = 1/4S.
б) По подобен начин се доказва, че SΔMPA = SΔNPB = 1/4S.
SΔMNP = SΔABC - (SΔMPA + SΔNPB + SΔMNC) = S - 3/4S = 1/4S.
Задача 24.
От точка A външна за окръжност k, са построени допирателна АВ и секателна АD (C е между A и D). Намерете:
а) CD, ако AB = 2, AD = 4;
б) AD, ако AC:CD = 4:5 и AB = 12.
Използвайте едната от готови конструкции с приложение на I признак.

ΔADB ~ ΔABC (по I ризнак, по 7 готова конструкция от теория) => AD/AB = BD/BC = AB/AC (1)
а) Нека CD = x, тогава AC = AD - CD = 4 - x, от (1) =>
AD/AB = AB/AC => 4/2 = 2/(4-x) => x = CD = 3.
б) От условие AC : CD = 4 : 5 => AC = 4x, CD = 5x, тогава AD = 4x + 5x = 9x и от (1) =>
AB/AB = AB/AC => 9x/12 = 12/4x => x = 1/3, т.е. AD = 9x = 3.
Задача 25.
В правоъгълен триъгълник ABC, катет AB = 21 см, а катет ВC = 28 см. Окръжност, центъра O на която лежи на хипотенузата AC,
допира и двата катета. Намерете радиуса на окръжността.
Предположите, че точка P - точка на допиране на страната BC. Тогава може да разгледате подобни триъгълници CPO и CBA.
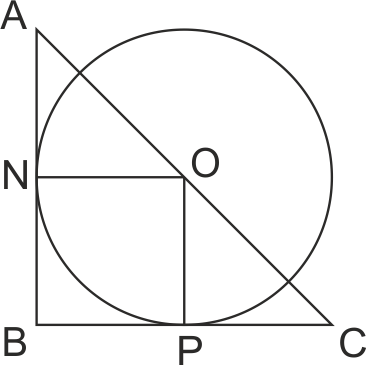
Ако kxBC = P, то ΔCPO ~ ΔCBA по II признак, защото ∠C - общ, ∠CPO = ∠CBA = 90o.
OPBN - квадрат => BP = R, OP = R.
PC/OP = BC/AB => (28-R)/R = 28/21 => R = 12.
Задача 26.
В триъгълник ABC прекарана права BD така, че ∠ABD = ∠ BCA. Намерете отсечки AD и DC, ако AB = 2 и AC = 4.
Използвайте, че ΔABD ~ ΔACB.
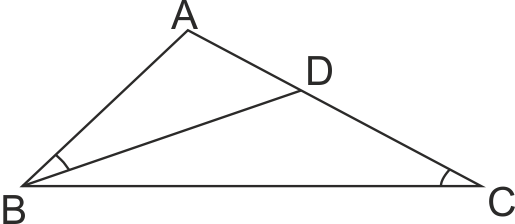
ΔABD ~ ΔACB (по II признак, ∠A - общ, ∠ABD = ∠BCA). Затова AD/AB = AB/AC.
Следователно AD = (AB)2/AC = 4/4 = 1; CD = AC - AD = 4 - 1 = 3.
Задача 27.
Диагоналите на четириъгълник ABCD се пресичат в точка O. Докажете, че AO*BO = CO*DO тогава и само тогава, когато BC || AD.
Използвайте I и II признаци за подобност.
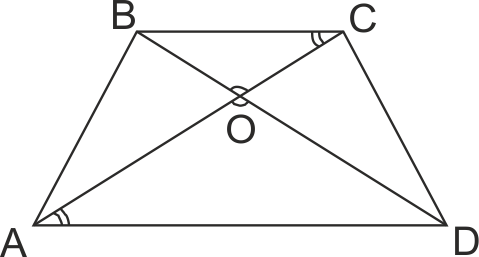
Ако BC || AD, то триъгълниците BOC и DOA са подобни по двата ъгъла (I признак) ∠O - общ, ∠ACB = ∠CAD (връхни),
затова BO/OD = CO/OA. Следователно OA*BO = CO*DO.
Обратно, ако OA*BO = CO*DO, то BO/OD = CO/OA и триъгълници BOC и DOA са подобни по двете пропорционални страни
и ъгъл заключен между тях (II признак). От тук ∠BCO = ∠DAO. Следователно, BC || AD.
Задача 28.
В успоредник ABCD точка N ∈ AB, точка M ∈ BC и AN : NB = 3 : 2, BM : MC = 2 : 5. Права AM и DN пресичатся в точка O.
Намерете отношенията OM : OA, ON : OD.
Продължете DN до пресичане с права BC и разгледайте 2 двойки подобни триъгълници.
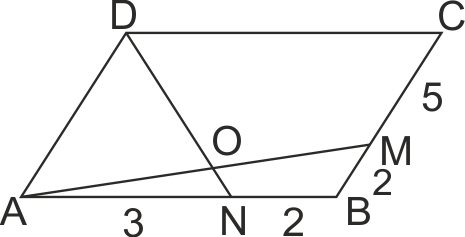
Продължаваме DN до BC, DNxBC = T. Полагаме BM = 2a, CM = 5a.
От ΔTNB ~ ΔDNA (k=2/3) намираме, че TB = 2/3AD = 2/3BC = 2/3*7a = (14/3)a, а от
ΔTOM ~ ΔDOA => OM/OA = TM/AD = ((14/3)a + 2a)/7a = 20/21.
Аналогично намираме ON/OD. ON/OD = 6/35.
Задача 29.
В ΔABC височина CH ⊥ AB, CD = d = 2R (R - радиус на описаната окръжност).
Да се докаже, че AC*BC = CD*CH.
Докажете, че ΔCHB ~ ΔCAD. Използвайте II признак за подобие.
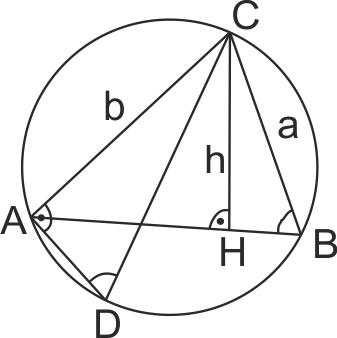
Разгледаме ΔCHB и ΔCAD.
∠A = ∠H = 90o, ∠B = ∠D = 1/2 от дъга AC (като вписани ъгли) => ΔCHB и ΔCAD.
Тогава CH/CA = CB/CD, откъдето CA*CB = CD*CH. Ако означим CA=b CB=a и CH=h, полученото равенство добива
вида ab = 2Rh.
Задача 30.
Да се изчисли растоянието AX между достъпната точка А и недостъпната точка X,
ако AB = а = 200 м, MB = b = 30 м, MN = m = 15 м. и ∠M = ∠A.
Приложете I признак за подобие, по сигурно едната от готови конструкции.
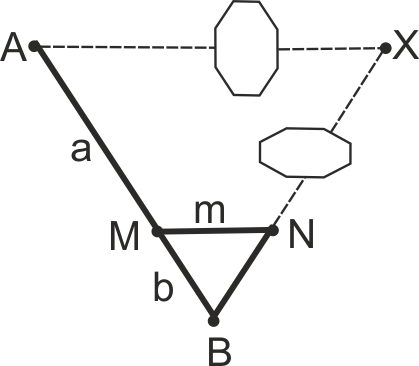
От подобие на ΔBMN и ΔBAX (1 готова конструкция от теория с приложение на I признак) имаме
AX : MN = AB : MB т.е. AX = (AB*MN)/MB => 15*200/30 = 100. AX = 100 м.
<<< 1
2 3 4
5 >>>









