<<< 1
2 3 4
5 >>>
Задача 11.
В ΔABC AB = 15, BC = 9. BL е ъглополовяща на ∠ABC (L∈AC), като AL = 5. Намерете страната AC на ΔABC.
Използвайте свойството на ъглополовящата.
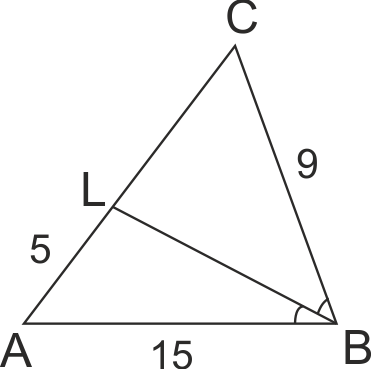
От свойството на ъглополовяща имаме AB/CD = AL/CL, ∠ABL = ∠CBL => ΔABL ~ ΔCBL.
От отношението получаваме 15/9 = 5/CL => CL = 45/15 => CL = 3 см.
Задача 12.
Точка M е медицентър на ΔABC. Права през точка M успоредна на BC пресича АC и AB в точки P и Q.
SCPQ = 20. Намерете SABC.
Използвайте II признак за подобие и 2 теорема от "Теория" от раздела "Лица на подобни многоъгълници".
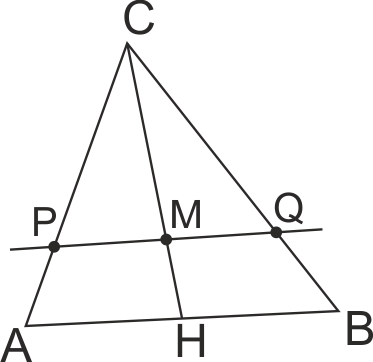
∠ACB - общ, CP / CA = CQ/CB => ΔABC ~ ΔPQC по II признак. SABC = k2SCPQ.
Но на нас не е дадена нито една страна, зацелта ще използваме отношение на друга двойка съответни линейнни елементи.
Имаме медицънтър М, тогава CH : CM = 3 : 2 = k => SABC = k2SCPQ = (9/4)*20 => SABC = 45 см2
Задача 13.
В трапец ABCD (AB || CD, AB<CD ) ACxDB = M така, че DM = 12, BM = 6 и AB = 8. Намерете основата CD на трапеца.
Използвайте I ризнак за подобие.
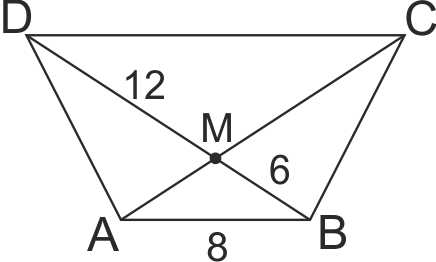
Разглеждаме триъгълници ABM и CDM.
∠BAM = ∠DCM (като връхни), a ∠AMB = ∠CMD (като кръстни) => по I признак ΔABM ~ ΔCDM.
AB/CD = BM/DM => 8/CD = 6/12 => CD = 96/6 => CD = 16.
Задача 14.
Даден е равнобедрен триъгълник с основа 6 см, бедро 5 см и височина към основата 4 см. Намерете радиуса на вписаната в
триъгълник окръжност.
Центъра на вписана окръжност в триъгълника е пресечна точка на ъглополовящите в триъгълника.
Приложете свойсвото на ъглополовяща.

Построяваме височина CH и ъглополовяща AO. OH = r. От пропорцията OH/OC = AH/AC => r/4-r = 3/5 => r = 3/2 или r = 1,5.
Задача 15.
Радиусът на описаната около равнобедрен триъгълник окръжност е 4 см, а височината към основата е 6 см. Намерете бедрото на триъгълника.
Центъра на описаната окръжност около Δ е пресечна точка на симетралите му. Докажете, че ΔCOS = ΔCAH.
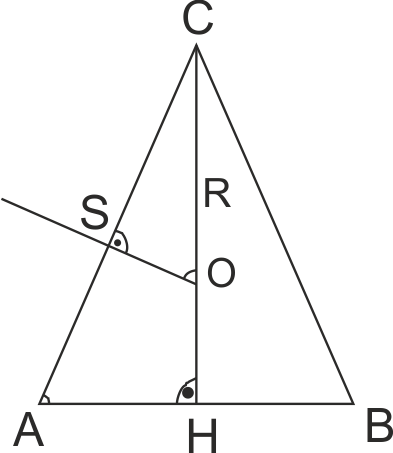
∠C - общ, ∠AHC = ∠OSC => ΔCOS ~ ΔCAH по I признак.
От пропорцията OC/AC = CS/CH намираме AC = 4√3.
Задача 16.
Периметърът на ΔABC е 50. CL е ъглополовяща на ∠ACB (L ∈ AB), като AL = 4, BL = 6. Намерете страните AC и BC.
Използвайте свойството на ъглополовящата.
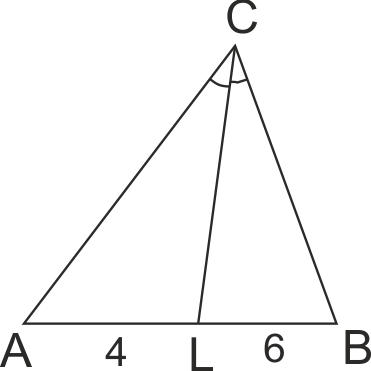
AC/CB = AL/LB, CL -обща страна и ∠ACL = ∠BCL; => ΔACL ~ ΔBCL по II признак.
От пропорция AC/CB = AL/LB => AC/CB = 4/6 = 2/3 => 3AC = 2CB или AC=3x, BC=2x.
PABC = AB + AC + BC = 50 => AC + BC = 40 => 5x=40 => x = 8.
AC = 24, BC = 16.
Задача 17.
В триъгълник ABC височините към страните BC и AC са съответно AP и BQ. ДОкажете, че ΔABC ~ ΔPQC.
Докажете, че ΔAPC ~ ΔBQC.
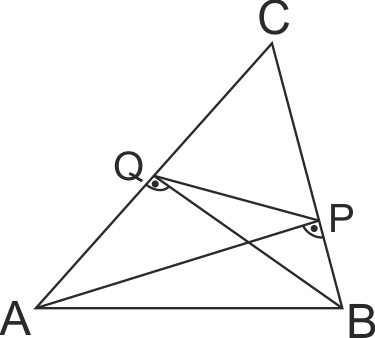
Разглеждаме ΔAPC и ΔBQC. ∠C - общ, ∠APC = ∠BQC = 90o - ΔAPC ~ ΔBQC по I признак.
От пропорцията AC/BC = PQ/QC и общ ∠C => ΔABC и ΔPQC по II признак.
Задача 18.
ΔABC ~ ΔMNP AB = 12, a MN = 16. Намерете отношението на ъглополовящите на ∠BAC към ∠NMP.
Използвайте едната от теореми на ъглополовящата.

От ΔABC ~ ΔMNP => AB/MN = AL/MK => 12/16 = AL/MK => AL/MK = 3/4 или MK/AL = 4/3.
Задача 19.
В триъгълника ABC точка D лежи на странат BC и е такава, че ∠BAD = ∠ACB. Намерете BD и DC, ако AB = 12 см, BC = 16 см.
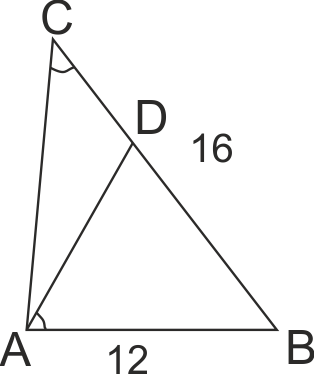
Разглеждаме триъгълници ΔABD и ΔCBA.
∠B - общ и ∠BAD = ∠ACB (по условие) => ΔABD ~ ΔCBA по I признак.
От пропорцията AB/BC = BD/AB намираме BD = 9. Тогава CD = CB - BD = 16 - 9 = 7.
Задача 20.
Даден е триъгълник ABC. Височината CD към страната AB я дели на части, отношението на които е 3 : 11. Намерете разстоянието
от медицентъра на триъгълника до височината CD, ако AB = 28 см.
Какво свойство притежава медицентъра на Δ ?
Постройте медиана CM, медицентър G (CG:GM = 2 : 1) и GH ⊥ CD. Докажете, че ΔCHG ~ ΔCDM.
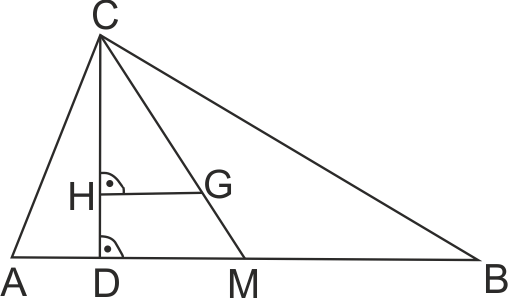
От GH ⊥ CD , MD ⊥ CD и HG || DM по Т. на Талес => ΔCHG ~ ΔCDM.
Тогава GH/DM = CG/CM = 2/3 (свойство на медицентър) (1)
От AB = 28 и AB = 14x => x = 2.
Тогава отсечка DM = AM - AD = AB/2 - AD = 4x = 8, DM = 8.
След заместване в пропорцията (1) се получава GH = 16/3.
<<< 1
2 3 4
5 >>>









