<<< 1
2 3 4
5 >>>
На следващите няколко страници са предложени различни видове задачи към теория с подробно решение към тях.
Задача 1.
Страните на един триъгълник са 6 см, 12 см и 10 см, а на друг - 18 см, 36 см и 30 см. Подобни ли са двата триъгълника?
Проверете дали съответните страни им са пропорционални.
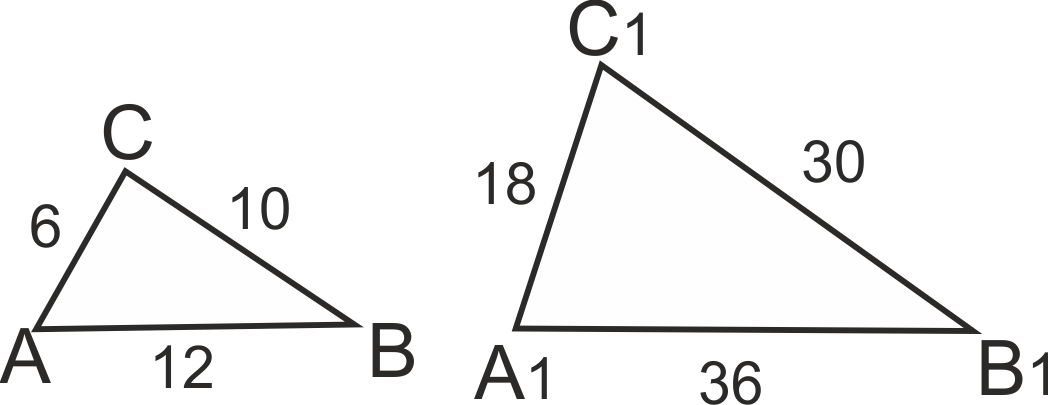
6/18 = 10/30 = 12/36 = 1/3 => подобни са по III признак.
Задача 2.
Катетът и хипотенузата на един правоъгълен триъгълник са съответно 3 см и 5 см, а
на друг правоъгълен триъгълник - 6 см и 11 см. Подобни ли са двата триъгълника?
Проверете дали съответните страни им са пропорционални.
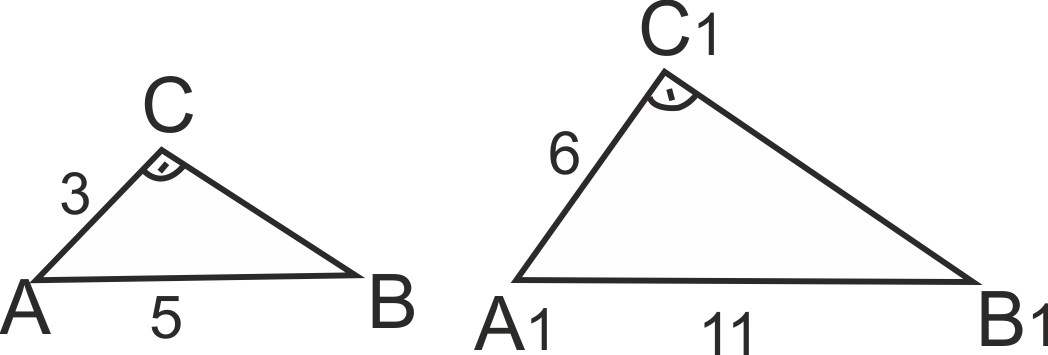
∠C = ∠C1, но 3/6 ≠ 5/11 => триъгълниците ABC и A1B1C1 не са подобни.
Задача 3.
Дадени са два подобни триъгълника ABC и A1B1C1. Периметърът на триъгълника ABC е три пъти
по-голям от периметъра на на триъгълника A1B1C1, а сборът на медианите АМ и A1M1
е 15 см. Намерете дължината на медианите на двата триъгълника.
Използвайте условието, че отношенията на всяка вдойка съответни линейни елементи на триъгълниците
са равни на коефициента на подобие k.
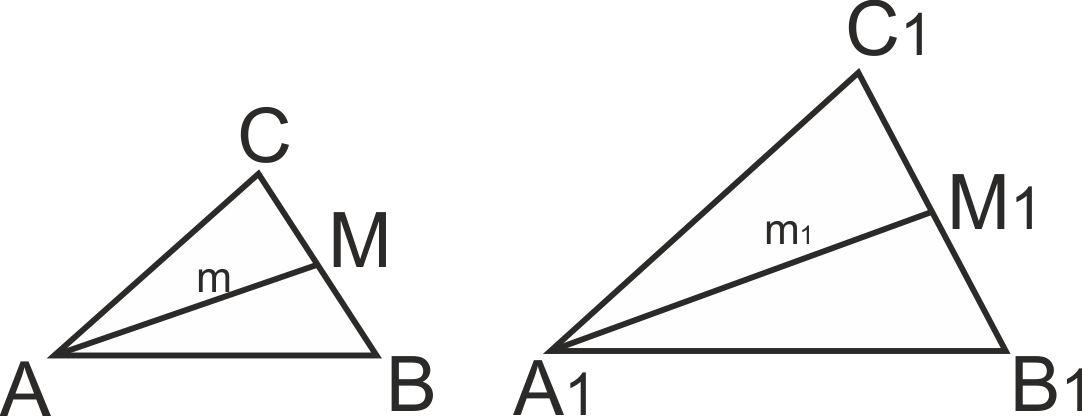
От условието, че ΔABC ~ ΔA1B1C1 =>
P/P1 = m/m1 = k = 1/3
Означаваме m = x, m1 = 3x.
От условие, че m + m1 = 15, получаваме x + 3x = 15 => x=15/4.
Следователно m = 15/4 m1 = 45/4.
Т.е. AM = 15/4, A1M1 = 45/4.
Задача 4.
Дадени са два подобни триъгълника. Периметър на единия е два пъти по-голям от периметъра на другия, а сборът
от квадратите на дължините на две съответни медиани е 125. Намерете тези медиани.
Използвайте условието, че отношенията на всяка вдойка съответни линейни елементи на триъгълниците
са равни на коефициента на подобие k.
От условие P/P1 = 1/2 => m/m1 = 1/2.
Означаваме m = x, m1 = 2x.
От уравнение m2 + m12 = 125 получаваме x2 + (2x)2 = 125,
т.е. x2 = 25 > x = 5. Тогава m = 5, m1 = 10.
Задача 5.
Даден е триъгълник ABC, за който AB = 10 см, AC = 12 см. Точката Q ∈ AB и QB = 4 см,
точката P ∈ AC и AP = 5 см. Точката M е средата на AB, а N е средата на AP. Намерете отношението CM : QN.
Докажете, че ΔAQN ~ ΔACM.
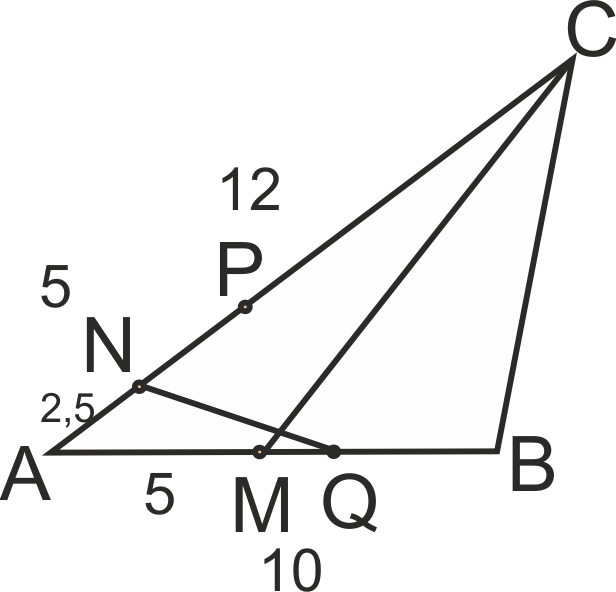
Пресмятаме дължините на отсечки: AN = 1/2AP = 2,5 см., AM = 1/2AB = 5 см., AQ = AB - QB = 6 см.
Разглеждаме триъгълници ACM и AQN:
От AN/AM = AQ/AC = 2,5/5 = 6/12 = 1/2 и ∠A - общ. =>
ΔAQN ~ ΔACM. Тогава CM : QN = 2/1.
Задача 6.
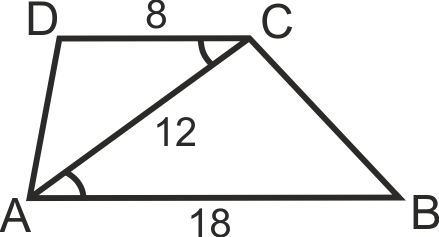
Основите на трапец ABCD с периметър 41 см са AB = 18 см., CD = 8 см. Един от диагоналите е 12 см. Намерете бедрата ба трапеца.
Докажете, че ΔABC ~ ΔCAD.
Пресмятаме дължините на отсечки: AN = 1/2AP = 2,5 см., AM = 1/2AB = 5 см., AQ = AB - QB = 6 см.
Разглеждаме триъгълници ABC и CAD:
∠BAC = ∠ACD (като връхни).
AB/AC = 18/12 = 3/2; AC/CD = 12/8 = 3/2.
По II признак за подобност => ΔABC ~ ΔCAD, от където следва, че BC/AD = 3/2.
Означаваме BC = 3x, AD = 2x. От PABCD = 41 см. се получава следното уравнение 5x + 26 = 41,
т.е. x = 3. Тогава AD = 6 см., BC = 9 см.
Задача 7.
Една от основите на трапец е 24 см., бедрата му са 9 см. и 12 см. Един от диагоналите разделя трапецана два подобни триъгълника.
Намерете този диагонал и втората основа на трапеца.
Определете, кой от ъглите на ΔABC съответства на ∠ADC от ΔADC.
Използвайте условието, че съответните страни на подобни триъгълници са пропорционални.
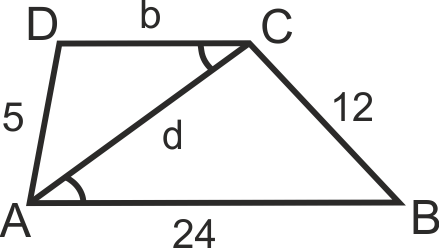
Тъй като не знаем коя от основите е равна на 24 см., то ще разгледаме 2 случая с решение на тази задача.
1 случай.
Разглеждаме триъгълниците ABC и CAD => AB/AC = BC/AD = AC/CD.
Ако AB = 24 см, то от пропорциите получаваме 24/d = 12/5 = d/b.
От пропорция 24/d = 12/5 намираме d, d = 24*5/12 => d = 10 см.
От пропорция 12/5 = d/b намираме b, b = 10*5/12 => b = 25/6 см.
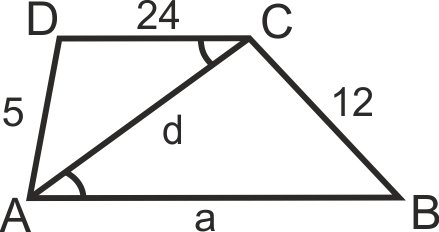2 случай.
Отново разглеждаме триъгълниците ABC и CAD => AB
/AC = BC
/AD = AC
/CD.
Ако DC = 24 см, то от пропорциите получаваме a
/d = 12
/5 = d
/24.
От пропорция 12
/5 = d
/24 намираме d, d = 12*24/5 => b = 288
/5 см.
От пропорция a
/d = 12
/5 намираме a, a = 288*12/5*5 => a = 3456
/25 см.
Задача 8.
В триъгълник ABC е вписан квадрат МNPQ, като М и N лежат на страната AB, а P и Q съответно на BC и AC. Страната AB е 12 см.,
а височината на триъгълника към нея е 8 см. Намерете страната на квадрата.
Използвайте свойството, че отношение на всяка вдойка съответни страни на подобни ртиъгълниците е равно
на отношение на всяка друга двойка съответни линейни елементи на триъгълници.
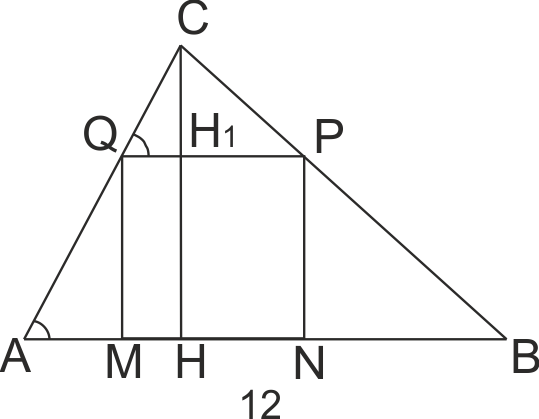
От ∠BAC = ∠PQC (кръстни) (QP || AB) и ∠C - общ => ΔABC ~ ΔQPC.
Означаваме страната на квадрата с a.
От пропорцията AB/QP = CH/CH1 намираме 12/a = 8/8-a => a=24/5.
Задача 9.
В триъгълник ABC със страните AB = 8 см, BC = 7 см, AC = 6 см, е вписан ромб AMNP, където M ∈ AB, N ∈ BC,
P ∈ AC. Намерете страната на ромба.
Какво свойство притяжава диагонала на ромба.
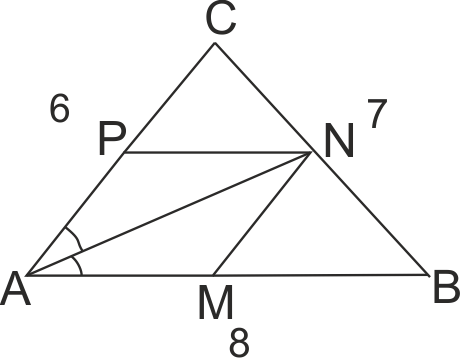
Построяваме диагонала AN на ромба AMNP.
От свойства на диагонала на рамба AN e ъглополоваща на ∠BAC. От тук => BN/CN = AB/AC.
Означаваме CN = x, BN = 7-x, заместваме в в горната пропорция и получаваме, че x = 3.
От ΔPNC ~ ΔABC следва PN/AB = CN/BC, PN/8 = 3/7. Тогава PN = 24/7.
Задача 10.
Катети на правоъгълен триъгълник ABC са AC = 3 см. и BC = 4 см. В триъгълник е вписан квадрат MNKP, където P и K ∈ AB,
N ∈ BC, M ∈ AC. Намерете страната на квадрата.
Използвайте свойството, че отношение на всяка вдойка съответни страни на подобни ртиъгълниците е равно
на отношение на всяка друга двойка съответни линейни елементи на триъгълници.
По питагорова теорема намираме AB, AB = √((AC)2+(BC))2 = 5 см.
ΔAPM ~ ΔNKB ~ ΔMCN и всеки от тях е подобен на ΔACB, но не са известни
страните на никой от тях.
Ще използваме отношение на друга двойка съответни линейни елементи. Построяваме CH - височина,
CH ∈ MN = H1. CH1 е височина на ΔMCN.
От метричната зависимост CH * AB = AC * BC <=> 5CH = 12 => CH = 12/5.
От ΔACB ~ ΔMCN съставяме пропорцията AB/MN = CH/CH1.Означаваме MN = a
=>
12/5*a = 5CH1 (1)
CH1 = CH - HH1, HH1 = a =>
CH1 = 12/5 - a (2)
От (1) и (2) => 12/5*a = 12 - a/5 => 13*a/5 = 12 => a = 60/13.
<<< 1
2 3 4
5 >>>
